Álgebra Linear Computacional

Aula 03: Quatro Subespaços Fundamentais

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento

Objetivos de Aprendizagem

1. Conhecer os 4 subespaços associados a uma matriz e suas relações
2. Identificar vetores que pertencem a cada subespaço
3. Saber definir vetores ortogonais e ortonormais

Referências adicionais

• Subespaços de A
  • Wikipedia
  • RGB Mathematics
• Forma mais rápida de encontrar subespaços de A

Os 4 subespaços fundamentais

• Espaço coluna: \(C(A)\)
• Espaço linha: \(C(A^\top)\)
• Espaço nulo: \(N(A)\)
• Espaço nulo esquerdo: \(N(A^\top)\)

\[A = \begin{bmatrix}1 & 2 \\ 3 & 6\end{bmatrix}\]

Espaço Coluna

• O espaço columa contém todas as combinações de coluna de \(A\)
• O espaço coluna da matriz \(A\) é a reta que passa pela origem e tem a direção \(u= \begin{bmatrix}1&3\end{bmatrix}^\top\)

Note

\(C(A) = \{Ax \mid x\in \mathbb R^2\}\)

Code

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.ticker as plticker
x = np.array(range(-3,4))
y = x*3 
plt.plot(x,y)
plt.grid(True)
plt.yticks(np.arange(-3, 4, 1.0))
axes=plt.gca()
axes.set_aspect(1)
plt.ylim([-3, 3])
plt.xlim([-3, 3])
plt.show()

Espaço Coluna

Espaço Linha

• O espaço linha contém todas as combinações das colunas de \(A\) transposta
• O espaço linha é a reta que contém a origem e a direção \(u = \begin{bmatrix}1 & 2\end{bmatrix}^\top\)

Note

\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 6\end{bmatrix}\] \[A^\top = \begin{bmatrix} 1 & 3 \\ 2 & 6\end{bmatrix}\]

\[C(A^\top) = \{A^\top v\mid v\in \mathbb R^2\}\]

Code

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.ticker as plticker
x = np.array(range(-3,4))
y = x*2 
plt.plot(x,y)
plt.grid(True)
plt.yticks(np.arange(-3, 4, 1.0))
axes=plt.gca()
axes.set_aspect(1)
plt.ylim([-3, 3])
plt.xlim([-3, 3])
plt.show()

Espaço Linha

Espaço Nulo

• Para quais valores de \(x\) a equação \(A x = 0\) é válida?

\[ Ax = x_1\begin{bmatrix}1\\3\end{bmatrix} + x_2\begin{bmatrix}2\\6\end{bmatrix} = 0\] \[ Ax = 2\begin{bmatrix}1\\3\end{bmatrix} + (-1)\begin{bmatrix}2\\6\end{bmatrix} = 0\] \[x = \begin{bmatrix}2 & -1\end{bmatrix}^\top \in N(A)\]

• O espaço nulo de \(A\) é a reta com direção \(x = \begin{bmatrix}2 & -1\end{bmatrix}^\top\)

Code

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.ticker as plticker
x = np.array(range(-3,4))
y = -x/2 
plt.plot(x,y)
plt.grid(True)
plt.yticks(np.arange(-3, 4, 1.0))
axes=plt.gca()
axes.set_aspect(1)
plt.ylim([-3, 3])
plt.xlim([-3, 3])
plt.show()

Espaço Nulo

Espaço Linha e Espaço Nulo

• Os espaço linha e nulo são ortogonais!

\[ Ax = \begin{bmatrix}1 & 2 \\ 3 & 6\end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix}= x_1\begin{bmatrix}1 \\ 3\end{bmatrix}+ x_2 \begin{bmatrix}2 \\ 6\end{bmatrix} = \begin{bmatrix}0 \\ 0\end{bmatrix}\] \[x\in N(A)\]

Espaço Nulo de \(A^\top\)

• \(N(A^\top)\) contém todas as soluções para a equação \[A^\top y = 0\]

• Também chamado de Left Nullspace

\[ Ax = y_1\begin{bmatrix}1\\2\end{bmatrix} + y_2\begin{bmatrix}3\\6\end{bmatrix} = 0\] \[ Ax = 3\begin{bmatrix}1\\2\end{bmatrix} + (-1)\begin{bmatrix}3\\6\end{bmatrix} = 0\] \[x = \begin{bmatrix}3 & -1\end{bmatrix}^\top \in N(A)\]

Code

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.ticker as plticker
x = np.array(range(-3,4))
y = -x/3
plt.plot(x,y)
plt.grid(True)
plt.yticks(np.arange(-3, 4, 1.0))
axes=plt.gca()
axes.set_aspect(1)
plt.ylim([-3, 3])
plt.xlim([-3, 3])
plt.show()

Espaço Nulo Esquerdo

Espaço Coluna e o Espaço Nulo de \(A^\top\)

• Os espaços e nulo de \(A^\top\) são ortogonais!

\[ A^\top y = \begin{bmatrix}1 & 3 \\ 2 & 6\end{bmatrix}\begin{bmatrix} y_1 \\ y_2\end{bmatrix} = y_1\begin{bmatrix}1 \\ 3\end{bmatrix}+ y_2 \begin{bmatrix}2 \\ 6\end{bmatrix} = \begin{bmatrix}0 \\ 0\end{bmatrix}\] \[y\in N(A^\top)\]

Os 4 Espaços Fundamentais

\[A = \begin{bmatrix}1 & 2 \\ 3 & 6\end{bmatrix}\] - \(A\) é um mapa \(f\colon \mathbb R^2 \rightarrow \mathbb R^2\) - Posto de \(A\) é 1 \[ C(A) = \begin{bmatrix}1 & 3\end{bmatrix}^\top \] \[ C(A^\top) = \begin{bmatrix}1 & 2\end{bmatrix}^\top \] \[ N(A) = \begin{bmatrix}2 & -1\end{bmatrix}^\top \] \[ N(A^\top) = \begin{bmatrix}3 & -1\end{bmatrix}^\top \]

Code

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.ticker as plticker
x = np.array(range(-3,4))
y = -x/3 
plt.plot(x,y)
# y = -2*x 
# plt.plot(x,y)
# y = x/2 
# plt.plot(x,y)
x = np.array(range(-1,2))
y = x*3 
plt.plot(x,y)
plt.grid(True)
plt.yticks(np.arange(-3, 4, 1.0))
axes=plt.gca()
axes.set_aspect(1)
plt.show()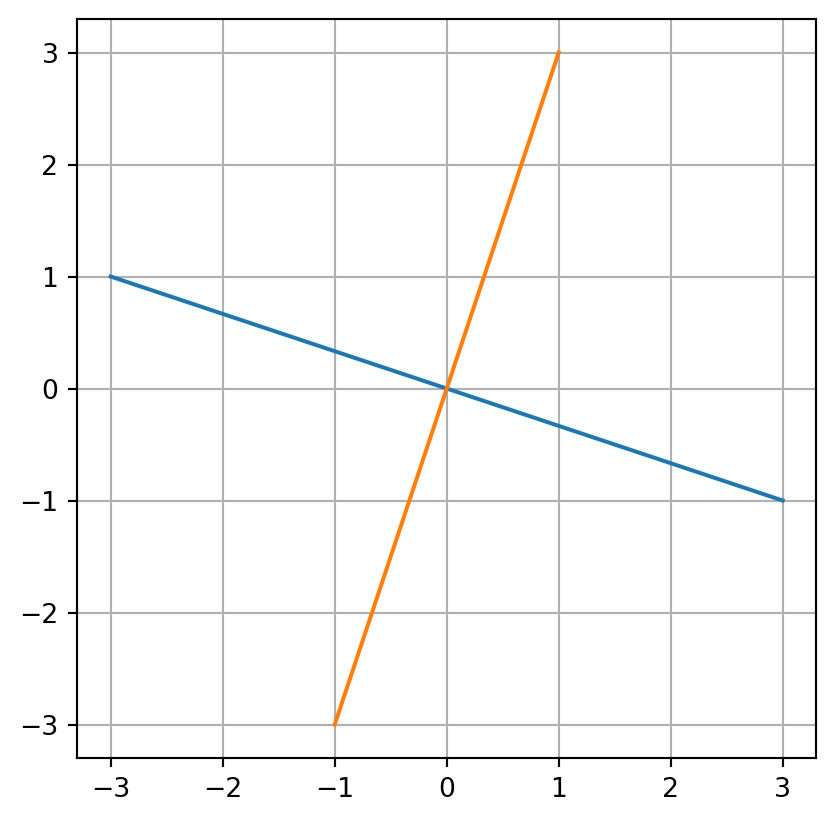

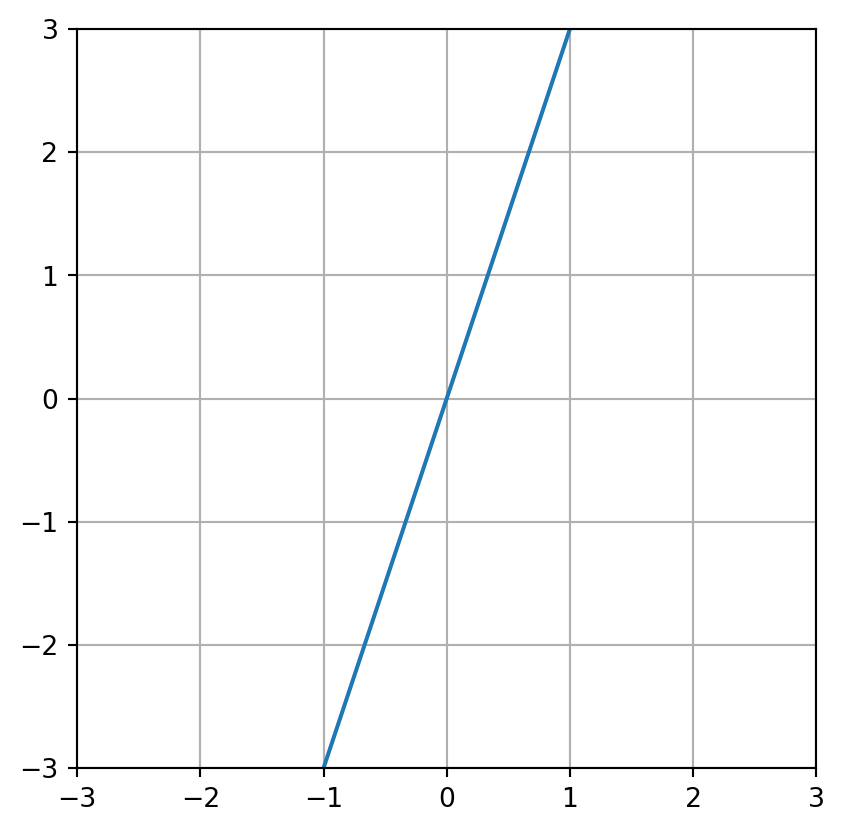
Espaço Coluna vs Espaço Nulo Esquerdo

Code

import matplotlib.pyplot as plt
import numpy as np
x = np.array(range(-3,4))
y = -x/2 
plt.plot(x,y)
x = np.array(range(-2,3))
y = 2*x
plt.plot(x,y)
plt.grid(True)
plt.yticks(np.arange(-3, 4, 1.0))
axes=plt.gca()
axes.set_aspect(1)
plt.ylim([-3, 3])
plt.show()

Espaço Linha vs Espaço Nulo

Exemplo 2

\[ B = \begin{bmatrix} 1 & -2 & -2 \\ 3 & -6 & -6\end{bmatrix}\]

• \(B\) tem 2 linhas e 3 colunas e alguns subespaçõs em \(\mathbb R^2\) e em \(\mathbb R^3\)
• De \(A\) para \(B\) dois subespaços se mantém e dois subespaços ficam diferentes
• \(C(B)\) e \(N(B^\top)\) continuam em \(\mathbb R^2\)
• Agora temos \(C(B^\top)\) e \(N(B)\) em \(\mathbb R^3\)
• Há apenas 1 vetor em \(C(B^\top)\) e o posto é 1
• Com \(n=3\) e o posto igual a 1, \(Bx=0\) tem \(3-1=2\) soluções independentes, \(x_1\) e \(x_2\)

\[ B = \begin{bmatrix} 1 & -2 & -2 \\ 3 & -6 & -6\end{bmatrix}\begin{bmatrix}a\\b\\c\end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix}\]

• A equação acima admite as seguintes soluções \[x_1 = \begin{bmatrix}2\\1\\0\end{bmatrix} \, x_2 = \begin{bmatrix}2\\0\\1\end{bmatrix}\]

• Essas não são as melhores soluções pois não são perpendiculares

• Aprenderemos como encontrar soluções perpendiculares através de Gram-Schmidt

Espaços linha e nulo de B: Linha perpendicular a um plano