Álgebra Linear Computacional

Aula 04: Autovalores e Autovetores

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento

Objetivos de Aprendizagem

  • Saber calcular autov* de matrizes \(2\times 2\) manualmente
  • Saber escrever polinômio característico para matrizes grandes e saber que suas raízes são os autovalores
  • Conhecer relação entre traço, determinante e autovalores
  • Conhecer relação entre autov* de \(A\), de \(A^k\), de \(A^{-1}\), e de \(A+sI\)
  • Saber definir matrizes similares e conhecer relação entre seus autov*
  • Saber que, quando existe, a decomposição espectral \(A=XΛ\) permite diagonalizar uma matriz
  • Saber calcular \(A^k\) e \(A^kv\) dada a decomposição \(A=XΛ\)

Referências

Multiplicação entre matrix e vetor

\[ \begin{bmatrix}2 & 1\\ 1 & 2\end{bmatrix}\begin{bmatrix}2\\3\end{bmatrix}=\begin{bmatrix}7\\8\end{bmatrix}\]

\[ 2\begin{bmatrix}2 \\ 1\end{bmatrix} + 3\begin{bmatrix}1 \\ 2\end{bmatrix}=\begin{bmatrix}7\\8\end{bmatrix}\]

Code 
import matplotlib.pyplot as plt
import numpy as np
V = np.array([[4,2], [3,6], [7,8],[2,1], [1,2],[4,2],[3,6],[2,3]])
origin = ([0,0,0,0,0,3,4,0],[0,0,0,0,0,6,2,0])
fig = plt.figure()
plt.quiver(*origin, V[:,0], V[:,1], angles='xy', scale_units='xy', scale=1, color=['red', 'red', 'green', 'gray','gray','blue','blue','yellow'])
plt.xlim((0,10))
plt.ylim((0,10)) 
plt.draw()
plt.show()

Produto Matrix x Vetor

Multiplicação entre matrix e vetor

\[ \begin{bmatrix}2 & 1\\ 1 & 2\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}=\begin{bmatrix}3\\3\end{bmatrix}\]

\[ 1\begin{bmatrix}2 \\ 1\end{bmatrix} + 1\begin{bmatrix}1 \\ 2\end{bmatrix}=3\begin{bmatrix}1\\1\end{bmatrix}\]

Code 
import matplotlib.pyplot as plt
import numpy as np
V = np.array([[1,2], [2,1], [3,3],[2,1],[1,2],[1,1]])
origin = ([0,0,0,1,2,0],[0,0,0,2,1,0])
fig = plt.figure()
plt.quiver(*origin, V[:,0], V[:,1], angles='xy', scale_units='xy', scale=1, color=['red', 'red', 'green','blue','blue','yellow'])
plt.xlim((0,4))
plt.ylim((0,4)) 
plt.draw()
plt.show()

Produto Matrix x Vetor

Note

Observe que nesse caso temos que \(Av = \lambda v\)

Autovalor e Autovetor

  • Seja \(A\) uma matriz quadrada \(m\times m\) \[Ax = \lambda x\]

Equação Característica

\[\begin{align}Ax -\lambda x &= 0\\ Ax -\lambda Ix &= 0\\ (A -\lambda I)x &= 0\\ det(M) &= 0, M = A- \lambda x\\ det((A - \lambda I)) &= 0 \rightarrow \text{Polinômio de grau } m \text{ em } \lambda \end{align}\]

Calculando Autovalores e Autovetores

\[ S = \begin{bmatrix}2 & 1\\ 1 & 2\end{bmatrix}\]

Polinômio Característico

  • Cálculo dos autovalores

\[M = S - \lambda I \\ M =\begin{bmatrix}2-\lambda & 1 \\ 1 & 2-\lambda\end{bmatrix} \\ det(M) = 0 \\ (2- \lambda)^2 -1 =0 \\ 4 - 4\lambda + \lambda^2 -1 =0 \\ \lambda^2 - 4 \lambda + 3=0 \\ \begin{cases} \lambda_1 =1 \\ \lambda_2 =3 \end{cases} \]

  • Cálculo dos autovetores \[\begin{align} Sx &= \lambda_1x & Sy &= \lambda_2 y\\ (S-\lambda_1 I)x &=0 & (S-\lambda_2 I)y &=0\\ \begin{bmatrix}1 & 1 \\ 1 & 1\end{bmatrix}x &=0 & \begin{bmatrix}-1 & 1 \\ 1 & -1\end{bmatrix}y &=0 \\ x_1\begin{bmatrix}1 \\ 1\end{bmatrix} + x_2\begin{bmatrix}1 \\ 1\end{bmatrix} &= 0 & y_1\begin{bmatrix}-1 \\ 1\end{bmatrix} + y_2\begin{bmatrix}1 \\ -1\end{bmatrix} &= 0\\ x &= \begin{bmatrix} 1\\-1\end{bmatrix} & y &= \begin{bmatrix} 1\\1\end{bmatrix} \end{align}\]

Traço, Determinante e Autovalores

  • Traço: Soma da diagonal da matriz - igual à soma dos autovalores

    \[ \text{trace}(A) = \text{tr}(A) = \sum_{i=1}^m \lambda_i\]

  • Determinante: Produto dos autovalores \[ det(A) = \mid A \mid = \prod_{i=1}^m \lambda_i\]

Autovalores Complexos

\[ R(\pi/2) = \begin{bmatrix}\cos(\pi/2)& -\sin(\pi/2)\\ \sin(\pi/2) & \cos(\pi/2)\end{bmatrix} = \begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix}\]

  • matriz que rotaciona \(90^\text{o}\) um vetor qualquer
  • claramente não tem autovalores reais (por quê?)

\[ det \left( \begin{bmatrix}-\lambda&-1\\1&-\lambda\end{bmatrix} \right) = 0 \\ \lambda^2 + 1 =0 \\ \lambda^2 = -1 \\ \begin{cases}\lambda = i\\ \lambda = -i\end{cases}\]

Potência da matriz A

  • \(x\) é autovetor de \(A \Leftrightarrow x\) é autovetor da matriz \(B = A^2\)

Prova

\[\begin{equation} Ax = \lambda x \Rightarrow A(Ax) = A(\lambda y)\\ A^2x = \lambda Ax\\ A^2x = \lambda (\lambda x)\\ A^2x = \lambda^2 x \end{equation}\]

\[ A^kx = \lambda^k x\]

Matriz inversa e autovalor

\[A^{-1}x = \frac{1}{\lambda}x\]

Prova

\[\begin{equation} Ax = \lambda x\\ A^{-1}Ax = \lambda A^{-1}x\\ Ix = \lambda A^{-1}x\\ A^{-1}x = \frac{1}{\lambda}x \end{equation}\]

O que acontece com os autovalores e autovetores de \(A\) se \(A\) for deslocada para \(A = A + sI\)?

\[ Ax = \lambda x\]

  1. Autovalores

    • considere \(\lambda'\) os autovalores de \(A+ sI\)
    • considere \(y\) autovetor de \(A + sI\) \[\begin{equation} (A+ sI)x = Ax + sx\\ (A+sI)x= \lambda x + sx\\ (A+sI)x = (\lambda + s)x\\ \text{observe que } \lambda+s = \lambda'\\ \end{equation}\]

  2. Autovetores \[\begin{equation} (A + sI)y = \lambda'y\\ (A + sI - \lambda'I)y = 0\\ (A - (\lambda' -s)I)y = 0\\ \text{observe que } \lambda'-s = \lambda\\ (A - \lambda I)y = 0 \end{equation}\]

Autovetores e a matriz \(A\)

  • Muitas matrizes \(n\times n\) possuem \(n\) autovetores independentes

    • nesse caso, um vetor \(v\) \(n\)-dimensional pode ser escrito como uma combinação dos autovetores

    \[ v = c_1x_1+\ldots + c_nx_n\]

    \[ Av = c_1\lambda_1x_1+\ldots + c_n\lambda_nx_n\]

Note

\[ Av = A(c_1x_1 + c_2x_2 + \ldots + c_nx_n)\\ Av = c_1Ax_1 + c_2Ax_2 + \ldots + c_nAx_n\\ Av = c_1\lambda_1x_1 + c_2\lambda_2x_2 + \ldots + c_n\lambda_nx_n\]

\[ A^2v = A(c_1\lambda_1x_1 + c_2\lambda_2x_2 + \ldots + c_n\lambda_nx_n)\\ A^2v = c_1\lambda_1Ax_1 + c_2\lambda_2Ax_2 + \ldots + c_n\lambda_nAx_n\\ A^2v = c_1\lambda_1^2x_1 + c_2\lambda_2^2x_2 + \ldots + c_n\lambda_n^2x_n\]

Autovetores e a matriz \(A\)

\[ A^kv = c_1\lambda_1^kx_1 + \ldots + c_n\lambda_n^kx_n\]

  • suponha que os autovalores ordenados apareçam da seguinte maneira

\[ \mid \lambda_1 \mid, \ldots, \mid \lambda_j\mid, \ldots, \mid \lambda_n\mid\]

  • suponha também que \(\mid \lambda_j \mid < 1\) e que \(\mid \lambda_1 \mid, \ldots, \mid\lambda_{j-1}\mid >1\)
  • nesse caso, se \(k \rightarrow \infty\) os termos a partir de \(\lambda_j\) ficam muito pequenos e a soma é dominada pelos primeiros termos

Matrizes Similares

  • Para toda matriz \(M\) inversível
    • \(B = M^{-1}AM\) tem os mesmos autovalores
    • \(B\) e \(A\) são matrizes similares

Note

\[ By = \lambda y \\ M(M^{-1}AM)y = M\lambda y \\ AMy = \lambda My \\ Ax = \lambda x\]

  • \(y\) é autovetor de \(B\)
  • \(x=My\) é autovetor de \(A\)

Diagonalização de matrizes

  • Seja uma matriz \(A\) \(n\times n\) com \(n\) autovetores (indep)

\[Ax = A\begin{bmatrix}\mid & \mid & \mid \\ x_1& \ldots& x_n \\ \mid & \mid & \mid\end{bmatrix} = \begin{bmatrix}\mid & \mid & \mid \\ Ax_1& \ldots& Ax_n \\ \mid & \mid & \mid\end{bmatrix}\]

\[Ax = \begin{bmatrix}\mid & \mid & \mid \\ \lambda_1x_1& \ldots& \lambda_1x_n \\ \mid & \mid & \mid\end{bmatrix} = \begin{bmatrix}\mid & \mid & \mid \\ x_1& \ldots& x_n \\ \mid & \mid & \mid\end{bmatrix}\begin{bmatrix}\lambda_1 & & \\ & \ddots& \\ & & \lambda_n\end{bmatrix}\]

Diagonalização de matrizes

\[A\begin{bmatrix}\mid & \mid & \mid \\ x_1& \ldots& x_n \\ \mid & \mid & \mid\end{bmatrix} = \begin{bmatrix}\mid & \mid & \mid \\ x_1& \ldots& x_n \\ \mid & \mid & \mid\end{bmatrix}\begin{bmatrix}\lambda_1 & & \\ & \ddots& \\ & & \lambda_n\end{bmatrix}\]

\[AX = X\Lambda\]

Note

\[AXX^{-1} = X\Lambda X^{-1}\\ A = X\Lambda X^{-1}\]

Diagonalização de matrizes

  • A matriz \(\Lambda\) é uma matriz diagonal com os autovalores

Diagonalização de matrizes

  • Como calcular \(A^k\)?

\[A = X\Lambda X^{-1}\]

Note

\[ A^2 = (X\Lambda X^{-1})(X\Lambda X^{-1})\\A^2 = X\Lambda^2 X^{-1} (A^2 \text{ é similar a } \Lambda^2)\]

  • Os autovalores de \(A^2\) são \(\lambda_1^2,\lambda_2^2, \ldots, \lambda_n^2\)

\[ A^k = X\Lambda^k X^{-1}\]

Exercício

Use:

Code 
import numpy as np
from numpy import linalg as LA
A = np.array([[.6,.2],[.4,.8]])
w,v = LA.eig(A)
w;v
v.dot(np.diag(w)**100).dot(LA.inv(v))
array([[0.33333333, 0.33333333],
       [0.66666667, 0.66666667]])

Note

Encontre os autovalores e autovetores das duas matrizes Markovianas \(A\) e \(A^\infty\). Use os cálculos para explicar o motivo de \(A^{100}\) ser tão próximo de \(A^\infty\)

\[ A = \begin{bmatrix}.6 & .2 \\ .4 & .8\end{bmatrix} \,\,\,A^\infty=\begin{bmatrix}1/3 & 1/3 \\ 2/3 & 2/3\end{bmatrix}\]

Exercício

  • Sequência de Fibonnacci: \(F(n) = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \ldots\)

  • Como saber o termo \(F(n)\), com \(n\in \mathbb N\) arbitrário sem resolver toda a sequência?

  • Iterativo:

Code 
#n = int(input("Que termo deseja encontrar: "))
n = 7
ultimo=1
penultimo=1


if (n==1) or (n==2):
    print("1")
else:
    count=3
    while count <= n:
        termo = ultimo + penultimo
        penultimo = ultimo
        ultimo = termo
        count += 1
    print(termo)
13
  • Recursivo
Code 
# Python program to display the Fibonacci sequence

def recur_fibo(n):
   if n <= 1:
       return n
   else:
       return(recur_fibo(n-1) + recur_fibo(n-2))

nterms = 10

# check if the number of terms is valid
if nterms <= 0:
   print("Plese enter a positive integer")
else:
   print("Fibonacci sequence:")
   for i in range(nterms):
       print(recur_fibo(i))
Fibonacci sequence:
0
1
1
2
3
5
8
13
21
34

Árvore de recursão Fib

Solução

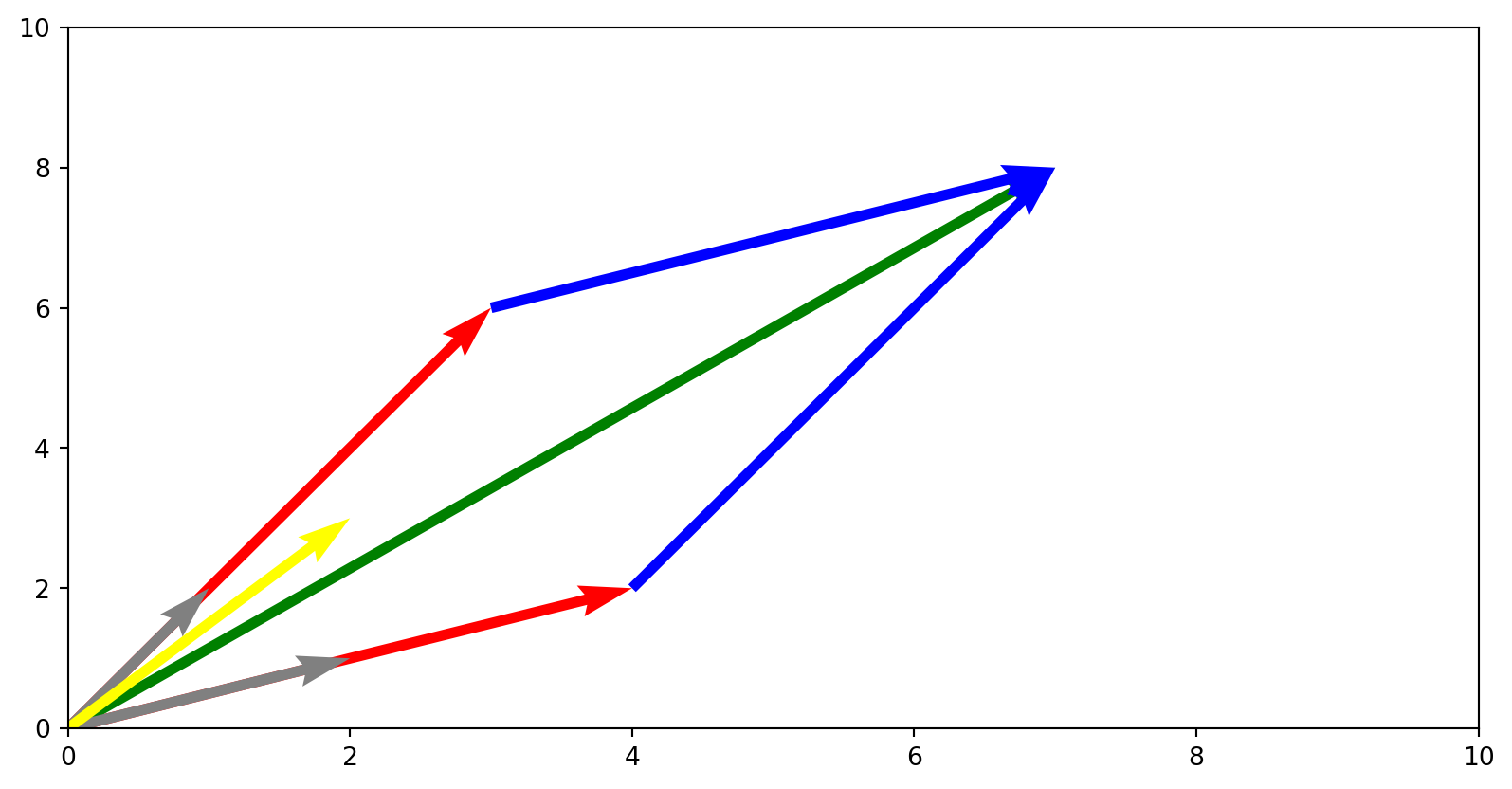
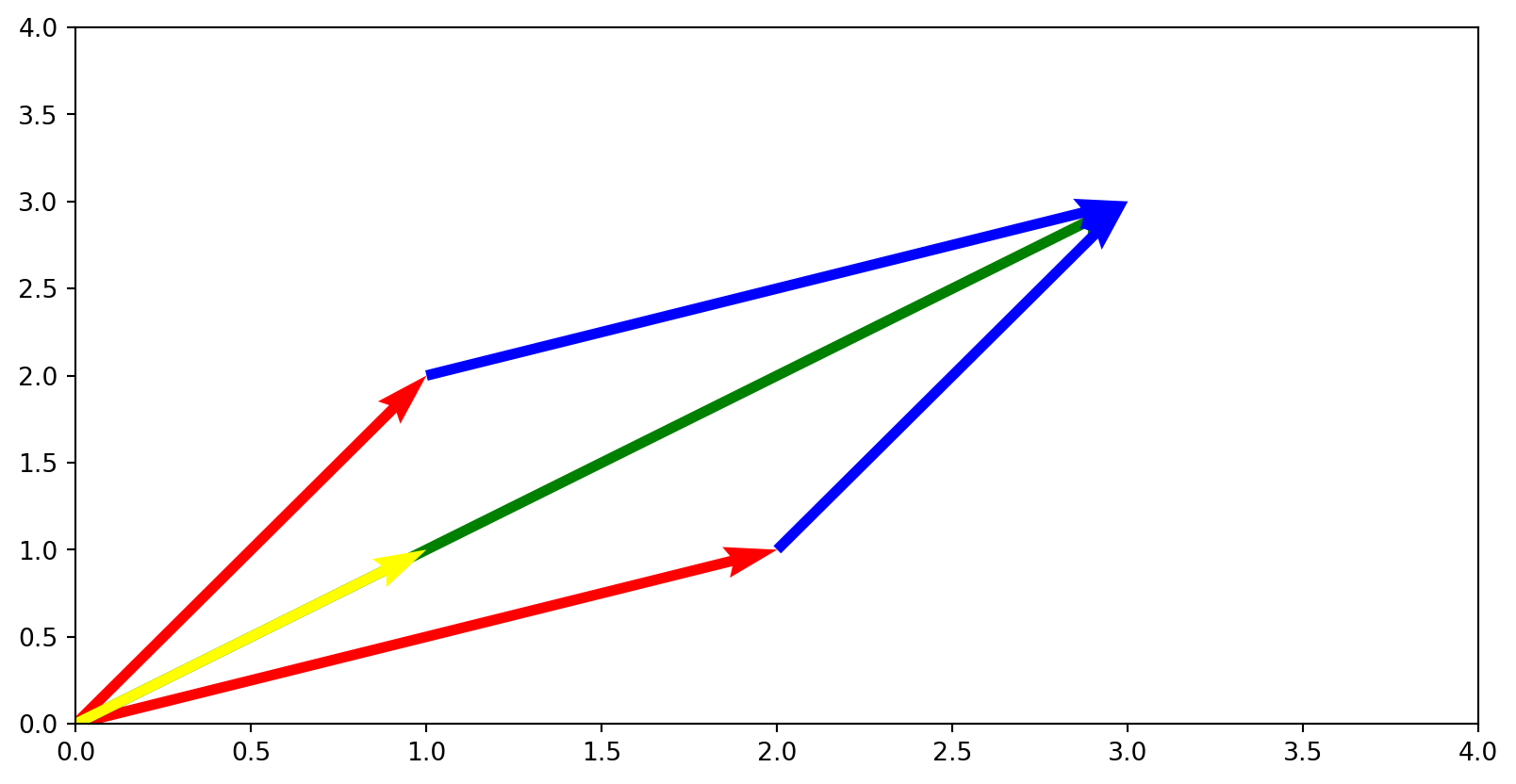
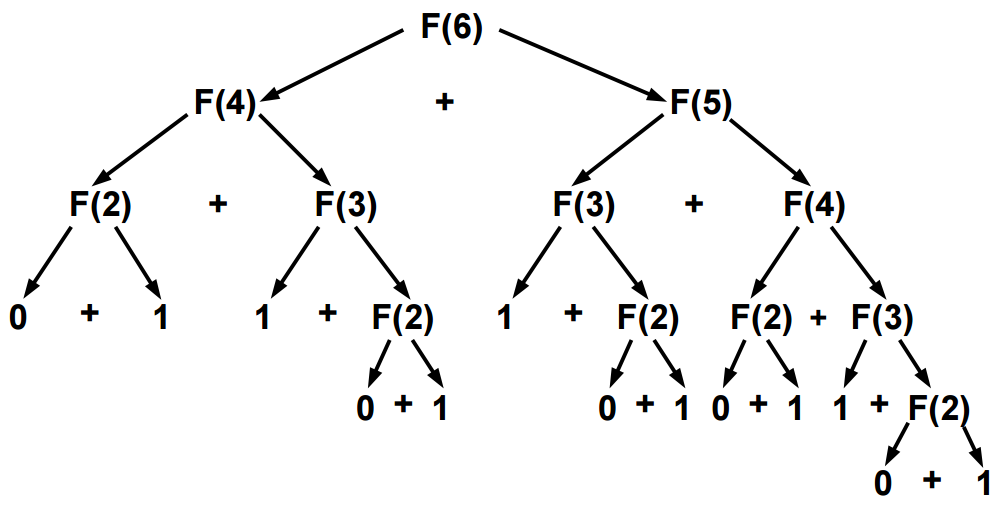
\[F(n+2) = F(n+1) + F(n)\]

\[ \begin{bmatrix}F(1) \\ F(2)\end{bmatrix} = \begin{bmatrix}1 \\ 1\end{bmatrix}\]

\[ \begin{bmatrix}F(2) \\ F(3)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}F(1) \\ F(2)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}1 \\ 1\end{bmatrix}\]

\[ \begin{bmatrix}F(3) \\ F(4)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}F(2) \\ F(3)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix}^{2} \begin{bmatrix}1 \\ 1\end{bmatrix}\]

\[ \begin{bmatrix}F(4) \\ F(5)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}F(3) \\ F(4)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix}^{3} \begin{bmatrix}1 \\ 1\end{bmatrix}\]

\[\vdots\]

\[ \begin{bmatrix}F(n) \\ F(n+1)\end{bmatrix} = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}F(2) \\ F(3)\end{bmatrix}= \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix}^{n-1} \begin{bmatrix}1 \\ 1\end{bmatrix}\]

  • considerando \(A = \begin{bmatrix}0 & 1 \\ 1 & 1\end{bmatrix}\), o problema se resume a resolver \(A^{n-1}\). Sabemos fazer essa conta?

  • Polinômio característico: \(\lambda^2 - \lambda -1=0\)

  • Autovalores: \[\lambda_1=\frac{1}{2} + \frac{1}{2}\sqrt{5}\] \[\lambda_2=\frac{1}{2} - \frac{1}{2}\sqrt{5}\]

  • Autovetores:

\[v_1 = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}x_1 \\ x_2\end{bmatrix} = \lambda_1\begin{bmatrix}x_1 \\ x_2\end{bmatrix}\]

\[v_2 = \begin{bmatrix}0 & 1 \\1 & 1\end{bmatrix} \begin{bmatrix}y_1 \\ y_2\end{bmatrix} = \lambda_2\begin{bmatrix}y_1 \\ y_2\end{bmatrix}\]

\[v_1 = x_1\begin{bmatrix}0 \\ 1\end{bmatrix} + x_2 \begin{bmatrix}1 \\ 1\end{bmatrix} = \left(\frac{1}{2} + \frac{1}{2}\sqrt{5}\right)\begin{bmatrix}x_1 \\ x_2\end{bmatrix}\]

\[v_2 = y_1\begin{bmatrix}0 \\ 1\end{bmatrix} + y_2 \begin{bmatrix}1 \\ 1\end{bmatrix} = \left(\frac{1}{2} - \frac{1}{2}\sqrt{5}\right)\begin{bmatrix}y_1 \\ y_2\end{bmatrix}\]

  • resolvendo o sistema acima (pode usar o pacote linag do python para calcular os autovalores e autovetores): \[ v_1 = \begin{bmatrix}1, & \frac{1}{2} + \frac{1}{2}\sqrt{5}\end{bmatrix}\]

\[ v_2 = \begin{bmatrix}1, & \frac{1}{2} - \frac{1}{2}\sqrt{5}\end{bmatrix}\]

  • Assim, podemos reescrever

\[ A^{n-1} = \begin{bmatrix}1 & 1 \\ \frac{1}{2} + \frac{1}{2}\sqrt{5} & \frac{1}{2} - \frac{1}{2}\sqrt{5}\end{bmatrix} \begin{bmatrix}\frac{1}{2} + \frac{1}{2}\sqrt{5} & 0 \\ 0 & \frac{1}{2} - \frac{1}{2}\sqrt{5}\end{bmatrix}^{n-1}\begin{bmatrix}1 & 1 \\ \frac{1}{2} + \frac{1}{2}\sqrt{5} & \frac{1}{2} - \frac{1}{2}\sqrt{5}\end{bmatrix}^{-1}\]

  • Sendo assim

\[\begin{bmatrix}F(n) \\ F(n+1)\end{bmatrix} = A^{n-1}\begin{bmatrix}1 \\ 1\end{bmatrix}\]

Code 
import numpy as np
import math
from numpy import linalg as LA

A = np.array([[1,1],[1/2+1/2*math.sqrt(5), 1/2-1/2*math.sqrt(5)]])

L = np.array([[1/2+1/2*math.sqrt(5),0],[0, 1/2-1/2*math.sqrt(5)]])
#n = int(input("Que termo deseja encontrar: "))
n = 7
Fn = A.dot((L**(n-1))).dot(LA.inv(A)).dot(np.array([[1],[1]]))

print(Fn)
[[13.]
 [21.]]

https://heitorramos.github.io/alc.html