Code
import matplotlib.pyplot as plt
import numpy as np
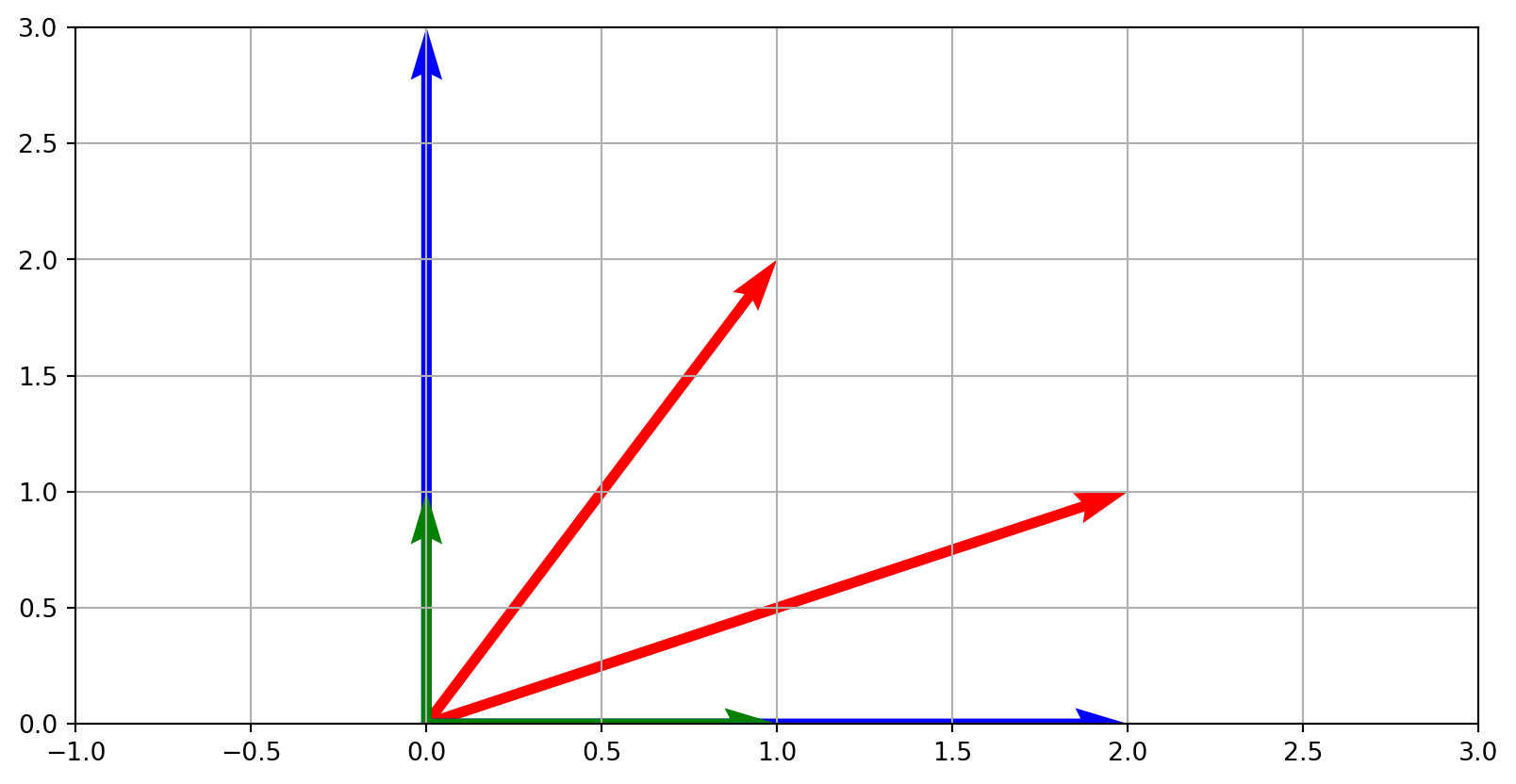
V = np.array([[1,2], [2,1], [2,0],[0,3], [1,0], [0,1]])
origin = ([0,0,0,0,0,0],[0,0,0,0,0,0])
fig = plt.figure()
plt.quiver(*origin, V[:,0], V[:,1], angles='xy', scale_units='xy', scale=1, color=['red', 'red', 'blue','blue', 'green', 'green'])
plt.xlim((-1,3))
plt.ylim((0,3))
plt.grid()
plt.show()