Álgebra Linear Computacional

Aula 07: Normas de Vetores e Matrizes - Parte II

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento.

Objetivos

Conhecer a definição de distância estatística
Conhecer relação entre normais vetoriais e normas matriciais induzidas
Saber calcular normas matriciais 1, 2, de Frobenius, infinito
Conhecer propriedades de normas matriciais
Saber interpretar a norma espectral (norma-2 matricial)

Referências adicionais

Wikipedia
- Normas matriciais
- Normas vetoriais
Youtube
- Chad Higdon-Topaz

Distância estatística

Precisamos de uma distância diferente da euclidiana para detectar anomalias em dados
Vamos começar vendo matrizes de dados estatísticos: matrizes com n items e k colunas ou variáveis

Exemplo 1

Relação entre força de preensão (do aperto de mão) e força do braço para 147 pessoas que trabalham em empregos fisicamente extenuantes

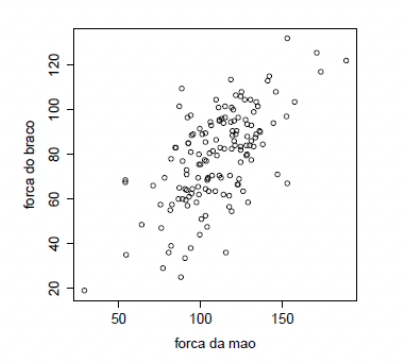
Matrizes de dados

Um vetor para cada indivíduo \(y = (y_1,y_2,\ldots,y_n)\)

As 9 variáveis são escores obtidos em 9 testes de habilidade cognitiva:

3 medindo habilidade verbal: Word Meaning, Sentence Completion, and Odd words
3 medindo habilidade quantitativa: Mixed Arithmetic, Remainders, and Missing numbers
3 medindo habilidade espacial: Gloves, Boots, and Hatchets

Matrizes de dados

Matriz de correlação

Matriz simétrica e definida positiva
Elemento \((i,j)\) mede o grau de associação linear entre um par de variáveis (diagonal 1, por quê?)

Desvio padrão

Desvio padrão (\(\sigma\)) é o tamanho médio do desvio de um dado para a média

Pressão sistólica

A pressão sistólica mede a força do sangue nas artérias à medida que o coração contrai para impulsionar o sangue
Se alta, ela pode levar à doença do coração, anginas e doenças vasculares nas pernas
Pressão sistólica saudável: entre 120 e 140 mmHg
Pressão sisólica > 140 mmHg: não saudável
Pressão diastólica deve ficar em torno de 80
Acima de 100 não é saudável

Pressão de 250 indivíduos

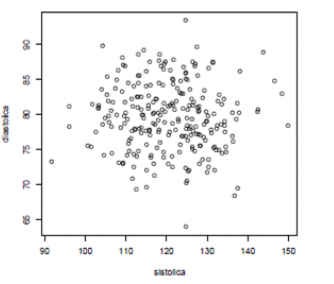
Amostra de \((y_{i1}, y_{i2})\), com \(i = 1,2,\ldots, 250\)

Médias para referência

250 instâncias do vetor aleatório: \(Y = (Y_1, Y_2)\)
Vetor com os valores esperados de cada variável: \[\mathbb E(Y) = \mathbb E(Y_1,Y_2) = (\mathbb E(Y_1), \mathbb E(Y_2)) = (\mu_1, \mu_2) = \mu\]

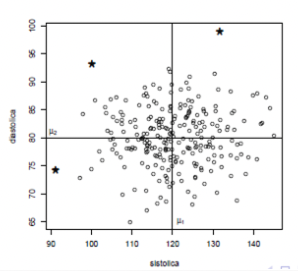
Quem está distante do esperado?

Centro \(\mu = (\mu_1, \mu_2)\) é o perfil esperado ou típico
Quem está longe do perfil típico? Quem é anômalo?
Medida baseada na distância euclidiana \(d(y_1,y_2) = \sqrt{(y_1-120)^2+ (y_2-80)^2}\)
é razoável?

Exagerando um pouco

E se o segundo atributo for assim? Fazendo o \(\text{aspect/ratio} = 1\).
Centro \(\mu = (\mu_1, \mu_2)\) continua o mesmo
Mas quem está distante do centro agora? Quem é anômalo?

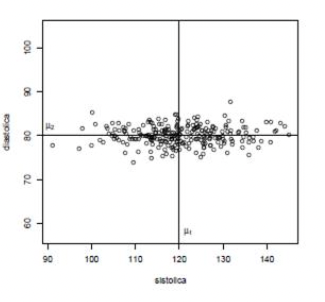
Distantes são óbvios, não?

Mas qual é a medida de distância que estamos usando sem ao mesmo perceber?
Não é a distância euclidiana!

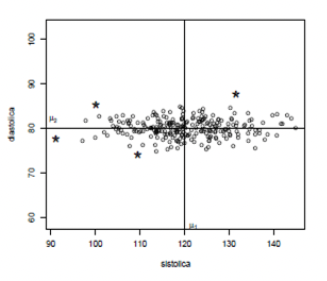
Pontos à igual distância

Todos os pontos do círculo estão à igual distância do centro da nuvem de pontos
Queremos os dois pontos em vermelho à igual distância ESTATÍSTICA do centro que os pontos em azul?
NÃO! Pontos vermelhos estão ESTATISTICAMENTE muito mais distantes do centro \((\mu_1, \mu_2)\) do que os pontos azuis

Pontos vermelhos mais distantes

Como fazer os pontos vermelhos mais distantes que os pontos azuis?
Andar poucas unidades na direção norte-sul te leva pra fora da nuvem dos pontos (vira anomalia)
Precisa andar MAIS unidades na direção leste-oeste para sair da nuvem de pontos

Pontos vermelhos mais distantes

Então \(N\) unidades euclidianas na direção leste-oeste valem o MESMO que \(N/k\) na direção norte-sul (onde \(k>1\))
Como achar esse \(k\)?
Como equalizar as distâncias?
Resposta: Medindo distâncias em unidades de DESVIOS PADRÕES

Distância Euclidiana

Medida de dispersão

Desvio padrão DP: um para cada eixo, um para cada atributo
DP mede quanto, em média, um atributo aleatório desvia-se do seue valor esperado
Por exemplo, \(DP=10\) significa:
- Em geral, observações desviam-se de 10 unidades em torno do seu valor esperado
- Às vezes mais de 10 unidades; às vezes menos de 10 unidades
- Em média, um afastamento de 10 unidades

Qual o desvio padrão de cada variável?

Centro \(\mathbb E(Y) = \mu = (\mu_1, \mu_2) = (120,80)\)
\(DP_1 = \sigma_1 = ??\)
\(DP_2 = \sigma_2 = ??\)

Qual o desvio padrão de cada variável?

Centro \(\mathbb E(Y) = \mu = (\mu_1, \mu_2) = (120,80)\)
\(DP_1 = \sigma_1 = 10\)
\(DP_2 = \sigma_2 = 2\)

Distância medida em DP

\((\mu_1,\mu_2) = (120,80)\) e \((\sigma_1, \sigma_2) = (10,2)\)
AZUL: afastou-se do centro apenas ao longo do eixo 1 e afastou-se \(15\) unidades, ou \(1.5\sigma_1\)
VERMELHO: afastou-se do centro apenas ao longo do eixo 2 e afastou-se \(15\) unidades ou \(7.5\sigma_2\)
o ponto VERMELHO está muito mais distante do centro em termos de DPs
Mas como fazer com pontos que afastam-se do centro não somente ao longo de um dos eixos?

Distância medida em DP

\((\mu_1,\mu_2) = (120,80)\) e \((\sigma_1, \sigma_2) = (10,2)\)
Andar \(n\sigma_1\) ao longo do eixo 1 é EQUIVALENTE a andar \(n\sigma_2\) no eixo 2
Por exemplo, 20 unidades ao longo do eixo 1 (ou \(2\sigma_1\)) é ESTATISTICAMENTE EQUIVALENTE a 4 unidades ao (ou \(2\sigma_2\)) longo do eixo 2

Distância medida em DP

Vamos medir o desvio em cada eixo EM UNIDADES DE DESVIO PADRÃO e calcular a distância com esses desvios padronizados
DESVIO PADRONIZADO ao longo do eixo 1 \[z_1 = \frac{y_1 - \mu_1}{\sigma_1}= \frac{y_1-120}{10}\]
DESVIO PADRONIZADO ao longo do eixo 2 \[z_2 = \frac{y_2 - \mu_2}{\sigma_2}= \frac{y_2-80}{2}\]
Distância:

\[\begin{align} d(y_1,y_2) &= \sqrt{z_1^2 + z_2^2} \\ &= \sqrt{\left(\frac{y_1-120}{10}\right)^2 + \left(\frac{y_2-80}{2}\right)^2} \\ &= \sqrt{\left(\frac{y_1-\mu_1}{\sigma_1}\right)^2 + \left(\frac{y_2-\mu_2}{\sigma_2}\right)^2} \\ \end{align}\]

Pontos a igual distância

NESSA NOVA MÉTRICA, quais os pontos \((y_1, y_2)\) que estão a uma MESMA distância do centro \((\mu_1, \mu_2)\)?
Tome uma distância fixa (por exemplo, 1)
Eles formam uma ELIPSE centrada em \((\mu_1, \mu_2)\) e com eixos paralelos aos eixos coordenados

\[ d(y, \mu) = \sqrt{\left(\frac{y_1-120}{10}\right)^2 + \left(\frac{y_2-80}{2}\right)^2} =1 \]

Tamanho dos eixos

Distância \(c>0\) do centro: pontos satisfazem a equação \[ d(y, \mu) = \sqrt{\left(\frac{y_1-120}{10}\right)^2 + \left(\frac{y_2-80}{2}\right)^2} =c \]
Os eixos têm comprimentos iguais a \(c\sigma_1\) e \(c\sigma_2\). O eixo maior da elipse: variável com maior DP
Quantas vezes o maior eixo é maior que o eixo menor?
Se \(\sigma_1\) é o maior DP, \[\frac{\text{eixo maior}}{\text{eixo menor}} = \frac{c\sigma_1}{c\sigma2} = \frac{\sigma1}{\sigma_2}\]
Não depende da distância \(c\). Ao variarmos \(c\) teremos elipses concêntricas

Variando a distância

Pontos \((y_1, y_2)\) que estão a uma distância \(c\) igual a 1, 2, 3 do centro \((\mu_1, \mu_2)\)

Jogando fora a raiz quadrada

Preferimos trabalhar com a distância AO QUADRADO
Se podemos complicar, por que simplificar?

\[\begin{align} d^2(y,\mu) &= \left(\frac{y_1-\mu_1}{\sigma_1}\right)^2 + \left(\frac{y_2-\mu_2}{\sigma_2}\right)^2 \\ &= \begin{bmatrix}y_1 - \mu_1& y_2- \mu_2\end{bmatrix} \begin{bmatrix}1/\sigma_1^2 & 0 \\ 0 & 1/\sigma_2^2\end{bmatrix}\begin{bmatrix}y_1 - \mu_1 \\ y_2 - \mu_2\end{bmatrix}\\ &= \begin{bmatrix}y_1 - \mu_1& y_2- \mu_2\end{bmatrix} \begin{bmatrix}\sigma_1^2 & 0 \\ 0 & \sigma_2^2\end{bmatrix}^{-1}\begin{bmatrix}y_1 - \mu_1 \\ y_2 - \mu_2\end{bmatrix}\\ &= (y-\mu)^\top \Sigma^{-1}(y-\mu) \end{align}\]

Elipses e distâncias

-Vimos que \[\begin{align} d^2(y,\mu) &= \left(\frac{y_1-\mu_1}{\sigma_1}\right)^2 + \left(\frac{y_2-\mu_2}{\sigma_2}\right)^2 \\ &= (y-\mu)^\top \Sigma^{-1}(y-\mu) \end{align}\] onde \[ \Sigma = \begin{bmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2\end{bmatrix}\] é a equação de uma elipse centrada em \(\mu = (\mu_1, \mu_2)\)

Quando a matriz \(\Sigma\) é DIAGONAL com elementos positivos (com as variâncias \(\sigma_i\)’s), então a elipse tem eixos paralelos aos eixos e o tamanho de cada eixo é proporcional ao \(\sigma_i\) da variável associada

Caso mais realista

Variáveis são associadas, não são independentes
Dizemos que são correlacionadas: redundância da informação
O valor de uma variável dá informação sobre o valor da outra variável
Pode-se predizer (com algum erro) uma variável em função da outra

Distância elíptica e não circular

Pelo mesmo raciocínio intuitivo que fizemos anteriormente, a ELIPSE abaixo tende a estar a igual distância do perfil esperado \(\mathbb E(Y) = \mu = (\mu_1,\mu_2)\)
Pontos estatisticamente equidistantes de \(\mu\) NÃO estão mais numa elipse paralela aos eixos
A elipse está inclinada seguindo a associação entre as variáveis

Forma quadrática

Medida de distância é uma FORMA QUADRÁTICA \[ d^2(y,\mu) = (y-\mu)^\top \Sigma^{-1}(y-\mu)\]
É a memsa expressão matricial de distância que usamos antes MAS…
… a matriz não é mais DIAGONAL

Quem é \(\Sigma\)?

Medida de distância é uma FORMA QUADRÁTICA \[ d^2(y,\mu) = (y-\mu)^\top \Sigma^{-1}(y-\mu)\]
Matriz \(\Sigma\) é uma matriz \(2\times 2\) simétrica chamada de matriz de covariância \[ \Sigma = \begin{bmatrix}\sigma_1^2 & \rho\sigma_1\sigma_2\\ \rho\sigma_1\sigma_2 & \sigma_2^2\end{bmatrix}\] onde \(\rho = \text{Corr}(Y_1, Y_2)\) é o índice de correlação de Pearson entre \(Y_1\) e \(Y_2\)
Temos sempre \(-1 \le \rho \le 1\)
Os elementos fora da diagonal, \(\rho\sigma_1\sigma_2\), são chamados de covariância entre \(Y_1\) e \(Y_2\)
Costumamos escrever \(\text{Cov}(Y_1,Y_2) = \rho\sigma_1\sigma_2 = \sigma_{12}\)

Relação entre \(\Sigma\) e a elipse

distância é \[ d^2(y,\mu) = (y-\mu)^\top \Sigma^{-1}(y-\mu)\] onde \(\Sigma\) é uma matriz \(2\times 2\) simétrica dada por \[ \Sigma = \begin{bmatrix}\sigma_1^2 & \rho\sigma_1\sigma_2\\ \rho\sigma_1\sigma_2 & \sigma_2^2\end{bmatrix}\]
Pontos equidistantes de \(\mu = (\mu_1, \mu_2)\) estão numa elipse
Eixos da elipse: na direção dos AUTOVETORES da matriz \(\Sigma^{-1}\)
O tamanho de cada eixo é proporcional à raiz do AUTOVALOR correspondente

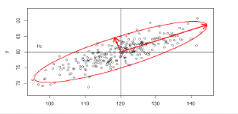
Autovetor e autovalor de \(\Sigma^{-1}\)

Na nossa situação de distância estatística em que usamos a inversa da matriz de covariância como \(\Sigma^{-1}\) temos dois resultados especiais:
- sempre temos dois autovetores ORTOGONAIS entre si
- autovalores são sempre REAIS e POSTIVOS (e portanto podemos tomar sua raiz ou invertê-los)

Autovetores de \(\Sigma\) e \(\Sigma^{-1}\)

Os autovetores de \(\Sigma\) e \(\Sigma^{-1}\) são os mesmos

Prova

Suponha que \(v\) é autovetor de \(\Sigma\) com autovalor \(\lambda >0\): \[\Sigma v = \lambda v\] \[ \Sigma^{-1}\Sigma v = \Sigma^{-1} \lambda v\]

ou seja, \[ v = \lambda\Sigma^{-1} v\] ou ainda, como \(\lambda >0\), \[ \frac{1}{\lambda}v = \Sigma^{-1}v\]

Distância estatística em \(k\) dimensões

Seja \(Y = (Y_1, Y_2, \ldots, Y_k)\) um vetor aleatório de dimensão \(k\)
Seja \(\mu = (\mu_1, \mu_2, \ldots, \mu_k)\) seu VETOR-COLUNA de valores esperados
Seja \(\Sigma\) a matriz \(k\times k\) com a covariância \(\sigma_{ij} = \rho_{ij}\sigma_i\sigma_j\) onde \(\rho_{ij}\) é a correlação entre \(Y_i\) e \(Y_j\)
Distância estatística: \[ d^2(y,\mu) = (y-\mu)^\top \Sigma^{-1}(y-\mu)\]
Pontos equidistantes de \(\mu\) formam um elipsóide em \(k\) dimensões com eixos nas direções dos autovetores de \(\Sigma\) e com tamanhos proporcionais aos seus respectivos autovetores

Caso 3D

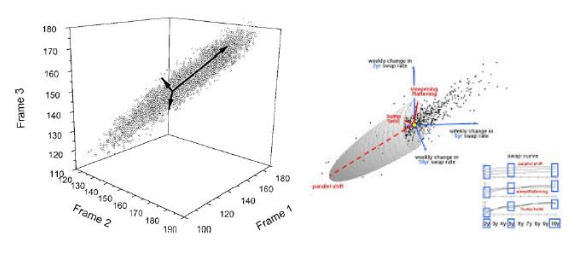
Distância estatística em \(k\) dimensões

\(\Sigma\) é a matriz de covariância \(k \times k\) de um vetor aleatório \(Y\) de dimensão \(k\), temos
- sempre temos \(k\) autovetores ORTOGONAIS entre si
- autovalores são sempre REAIS e POSITIVOS
Esta afirmação é consequência do teorema espectral
Para todo ponto \(y\) que não seja o vetor esperado \(\mu\), queremos que a distância \(d^2(y,\mu)\) seja \(>0\)
Uma matriz com essa propriedade é chamada de positiva definida

Norma-S

Seja \(S\) uma matriz simétrica e definida positiva

Definição Norma-S

\[\Vert x\Vert_S = x^\top S x = \sum_{i,j}x_ix_jS_{ij}\]

Norma de matrizes

Vamos querer comparar “tamanhos” de matrizes Como atribuir um tamanho para as matrizes abaixo?

\[\begin{bmatrix}0.1 &&\\ &0.2&\\&&0.3\end{bmatrix}\, \begin{bmatrix}150 &&\\ &150&\\&&180\end{bmatrix}\, \begin{bmatrix}100 &80&80\\ 90&150&100\\90&100&180\end{bmatrix}\]

Qual o tamanho? Quem é maior?

\[\begin{bmatrix}1 &&\\ &1&\\&&1\end{bmatrix}\, \begin{bmatrix}1000 &\\ &1000\end{bmatrix}\, \begin{bmatrix}1.3 &5.9&-1.6\\ 1.7&6.1&9.7\\2.7&9.1&1.2\\-0.4&2.7&2.8\\2.2&7.2&7.9\end{bmatrix}\]

Norma de Frobenius

A mais simples de todas: - Empilhe as colunas da matriz como um vetor e calcule sua norma L2

\[A = \begin{bmatrix}1.3&5.9&-1.8\\1.7&6.1&9.7\end{bmatrix}\] \[\Vert A\Vert_F = \sqrt{(1.3)^2+(5.9)^2+(-1.8)^2+(1.7)^2+(6.1)^2+(9.7)^2}\]

\[\Vert A\Vert_F = \sqrt{\sum_{ij}\vert a_{ij}\vert^2}\]

Frobenius via linha/coluna

Outras descrições úteis de Frobenius

\[A_{n\times m} = \begin{bmatrix}\vert&\vert&&\vert\\ a_1&a_2&\ldots&a_m\\\vert&\vert&&\vert\end{bmatrix} = \begin{bmatrix}-&b_1^\top&-\\-&b_2^\top&-\\&\vdots&\\ -&b_n^\top&-\end{bmatrix} \]

\[\begin{align} \Vert A \Vert_F^2 &= \sum_{ij}\vert a_{ij}\vert^2\\ &= \sum_{j=1}^m \Vert a_j\Vert_2^2\\ &= \sum_{i=1}^n \Vert b_i^\top\Vert_2^2\\ &= \text{trace}(A^\top A) \end{align}\]

Normas de matrizes

A norma de uma matriz é uma função \(\Vert \star\Vert\) do conjunto de todas as matrizes complexas (de todas as ordens finitas) para \(\mathbb R\) que satisfaz as seguintes propriedades

\(\Vert A\Vert \le 0\) e \(\Vert A \Vert = 0 \Leftrightarrow A = 0\)
\(\Vert \lambda A\Vert = \vert \lambda\vert \Vert A \Vert\) para todos escalar \(\lambda\)
\(\Vert A + B \Vert \le \Vert A \Vert + \Vert B \Vert\) para matrizes do mesmo tamanho
\(\Vert AB\Vert \le \Vert A \Vert \Vert B \Vert\) para todas as matriz compatíveis