Álgebra Linear Computacional

Aula 10: Decomposição por valores singulares

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento

Objetivos de aprendizagem

Conhecer relação entre posto, valores singulares e vetores singulares esquerdos e direitos de uma matriz
Saber transformar o SVD completo em SVD reduzido e vice-versa
Entender o SVD como uma decomposição em soma de matrizes de posto 1
Saber como calcular o SVD a partir da decomposição espectral de \(A^\top A\) ou \(AA^\top\) Entender a multiplicação \(Ax\) da perspectiva geométrica do SVD

Referências adicionais

E quando a matriz não é quadrada?

\[A = \begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}\]

\[y = \begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}\begin{bmatrix}10\\100\end{bmatrix} = 10\begin{bmatrix}1\\3\\5\end{bmatrix}+100\begin{bmatrix}2\\4\\6\end{bmatrix} = y\in \mathbb R^3\]

Exemplo de uma matriz tall-thin

Tall-thin matrix

E como ficam os autovetores?

Não é possível usarmos \[Ax=\lambda x\]

O que podemos fazer? Será que existem vetores escalares tais que

\[Av_i = \sigma_i u_i \]

Quantos vetores independentes de \(u_i\)?

Como \(u_i\) está em \(C(A)\), existem no máximo \(r\) vetores \(u_i\)’s independentes, onde \(r=\text{posto}(A) \le \min\{m,n\}\)

Note que sempre existe um \(v_i\) para cada \(u_i\)

\[Av_1 = \sigma_1 u_1\] \[Av_2 = \sigma_2 u_2\]

\[ \vdots\]

\[Av_r = \sigma_r u_r \]

Em forma matricial

\[A\begin{bmatrix}\vert & \vert & \ldots & \vert \\ v_1 & v_2 & \ldots & v_r\\\vert & \vert & \ldots & \vert \end{bmatrix} = \begin{bmatrix}\vert & \vert & \ldots & \vert \\ u_1 & u_2 & \ldots & u_r\\\vert & \vert & \ldots & \vert \end{bmatrix}\begin{bmatrix}\sigma_1 & & \\ &\ddots&\\&&\sigma_r\end{bmatrix} \]

Note

Essas dimensões correspondem ao SVD reduzido

Exemplo \(AV = U\Sigma\)

\[ \underbrace{ \begin{bmatrix} 3&0\\ 4&5 \end{bmatrix}}_A \underbrace{ \frac{1}{\sqrt{2}} \begin{bmatrix} 1&-1\\ 1&1 \end{bmatrix}}_V = \underbrace{ \frac{1}{\sqrt{10}} \begin{bmatrix} 1&-3\\ 3&1 \end{bmatrix}}_U \underbrace{ \begin{bmatrix} 3\sqrt{5}&\\ &\sqrt{5} \end{bmatrix}}_\Sigma \]

Tornando \(V\) quadrada

Se o espaço coluna \(C(A)\) tem dimensão \(r\), existem \(r\) vetores \(\sigma_iu_i\) independentes que podem ser escritos como \(Av_i\)

Sabemos ainda que o espaço nulo \(N(A)\) tem dimensão \(n-r\)

Logo, existem \(n-r\) vetores \(v_j\) independentes tais que \(Av_j=0\)

Esses vetores são orgotonais a \(v_1,\ldots,v_r\), concatenando-os a \(V\),

\[ A_{m\times n} \underbrace{ \begin{bmatrix} \vert & \ldots & \vert & & \vert& \ldots &\vert\\ v_1 &\ldots & v_r && v_{r+1} & \ldots & v_n\\ \vert & \ldots & \vert & & \vert& \ldots &\vert \end{bmatrix}}_{n\times n} = \underbrace{ \begin{bmatrix} \vert & \ldots & \vert\\ u_1 & \ldots & u_r\\ \vert & \ldots & \vert\\ \end{bmatrix}}_{m\times r} \underbrace{ \begin{bmatrix} \sigma_1 &\ldots & 0 && 0 &\ldots & 0\\ \vdots &\ddots & \vdots && \vdots &\ddots & \vdots\\ 0 &\ldots & \sigma_r && 0 &\ldots & 0\\ \end{bmatrix}}_{r\times n} \]

Tornando \(U\) quadrada

Como os vetores \(u_i\) estão no \(\mathbb R^m\), existem \(m-r\) vetores independentes \(u_j\) ortogonais a \(u_1, \ldots, u_r\). Logo, podemos concatená-los a \(U\), desde que sejam adicionadas \(m-r\) linhas nulas em \(\Sigma\):

\[ A_{m\times n} \underbrace{ \begin{bmatrix} \vert & \ldots & \vert & & \vert& \ldots &\vert\\ v_1 &\ldots & v_r && v_{r+1} & \ldots & v_n\\ \vert & \ldots & \vert & & \vert& \ldots &\vert \end{bmatrix}}_{n\times n} = \underbrace{ \begin{bmatrix} \vert & \ldots & \vert & & \vert& \ldots &\vert\\ u_1 & \ldots & u_r && u_{r+1} & \ldots & u_m\\ \vert & \ldots & \vert & & \vert& \ldots &\vert\\ \end{bmatrix}}_{m\times m} \underbrace{ \begin{bmatrix} \sigma_1 &\ldots & 0 && 0 &\ldots & 0\\ \vdots &\ddots & \vdots && \vdots &\ddots & \vdots\\ 0 &\ldots & \sigma_r && 0 &\ldots & 0\\ \\ 0 &\ldots & 0 && 0 &\ldots & 0\\ \vdots &\ddots & \vdots && \vdots &\ddots & \vdots\\ 0 &\ldots & 0 && 0 &\ldots & 0\\ \end{bmatrix}}_{m\times n} \]

Note

Essas dimensões correspondem ao SVD completo

Em forma matricial

Se todos os vetores \(v\)’s forem ortogonais (e eles são), podemos reescrever como

\[ AV = U \Sigma\]

\[ AVV^{-1} = U \Sigma V^{-1}\]

\[ A = U \Sigma V^\top\]

Do SVD completo ao reduzido

SVD Completo

\[\underbrace{A}_{m\times n} = \underbrace{U}_{m\times m} \underbrace{\Sigma}_{m\times n}\underbrace{V^\top}_{n\times n}\]

Como apenas os \(r\) primeiros termos da diagonal de \(\Sigma\) são não-nulos, podemos tomar essa submatriz descartando as colunas \(r+1,\ldots,m\) de \(U\) e as linhas \(r+1,\ldots,n\) de \(V^\top\). O resultado, denotado pelas mesmas letras é

SVD Reduzido

\[\underbrace{A}_{m\times n} = \underbrace{U}_{m\times r} \underbrace{\Sigma}_{r\times r}\underbrace{V^\top}_{r\times n}\]

Decomposição por valor singular

A decomposição \(A = U\Sigma V^\top\) é chamada de Singular Value Decomposition (SVD)

Os escalares na matriz \(\Sigma\) são os valores singulares
Os vetores coluna de \(U\) são os vetores singulares à esquerda
Os vetores coluna de \(V\) (ou seja, linhas de \(V^\top\)) são os vetores singulares à direita

SVD em “pedaços”

Podemos escrever a decomposição como soma de matrizes de posto 1

\[ A = U \Sigma V^\top = ?\]

\[ A = \begin{bmatrix} \vert &\vert & \ldots &\vert \\ \sigma_1u_1 & \sigma_2u_2 & \ldots & \sigma_ru_r \\ \vert &\vert & \ldots &\vert \\ \end{bmatrix} \begin{bmatrix} - & v_1^\top & -\\ - & v_2^\top & -\\ - & \vdots & -\\ - & v_r^\top & -\\ \end{bmatrix} \]

\[A = \sigma_1u_1v_1^\top + \ldots + \sigma_r u_r v_r^\top\]

Note

cada termo da soma acima é uma matriz \(m\times n\)

Observe que \(\begin{bmatrix}\sigma_1u_1\end{bmatrix}_{m\times 1}\) e que \(\begin{bmatrix}-&v_1^\top&-\end{bmatrix}_{1\times n}\)

Exemplo

\[ \underbrace{\frac{3\sqrt{5}}{\sqrt{10}\sqrt{2}} \begin{bmatrix} 1\\3 \end{bmatrix} \begin{bmatrix} 1 & 1 \end{bmatrix}}_{\sigma_1u_1v_1^\top} + \underbrace{\frac{\sqrt{5}}{\sqrt{10}\sqrt{2}} \begin{bmatrix} -3\\1 \end{bmatrix} \begin{bmatrix} -1 & 1 \end{bmatrix}}_{\sigma_2u_2v_2^\top} \]

\[ = \frac{3}{2} \begin{bmatrix} 1&1\\3&3 \end{bmatrix} + \frac{1}{2} \begin{bmatrix} 3&-3\\-1&1 \end{bmatrix} = \underbrace{\begin{bmatrix} 3&0\\4&5 \end{bmatrix}}_{A} \]

Note

Como os vetores \(u_i\) e \(v_i^\top\) têm norma 1, então \(u_1\) será dividido por \(\sqrt{10}\) e \(v_1^\top\) por \(\sqrt{2}\). Sendo assim, \(\sigma_1 = 3\sqrt{5}\). O mesmo procedimento pode ser empregado no segundo termo para chegar a \(\sigma_2=\sqrt{5}\).

Autovalores e valores singulares

Existe alguma relação entre autovalores e valores singulares?

\[A = U\Sigma V^\top\] \[S = X\Lambda X^{-1} \]

Autovalores e valores singulares

Existe alguma relação entre autovalores e valores singulares?

Sim, 2 matrizes simétricas

\[A^\top A = ?\]

Como \(A = U\Sigma V^\top\)

\[\begin{align} A^\top A &= (U\Sigma V^\top)^\top U\Sigma V^\top \\ &= V\Sigma \underbrace{U^\top U}_{I}\Sigma V^\top \\ &= V\Sigma^2 V^\top \\ &= \underbrace{ \begin{bmatrix} \vert & \ldots & \vert \\ v_1 & \ldots & v_r \\ \vert & \ldots & \vert \end{bmatrix}}_{Q} \underbrace{ \begin{bmatrix} \sigma_1^2 && \\ & \ddots & \\ && \sigma_r^2 \end{bmatrix}}_{\Lambda} \underbrace{\begin{bmatrix} - & v_1 & - \\ - & \vdots &- \\ - & v_r & - \end{bmatrix}}_{Q} \end{align}\]

Observe que como \(S = A^\top A\), e \(S\) é simétrica, então \(S = Q\Lambda Q^\top\)

Note

Autovalores de \(S = A^\top A\) são valores singulares de \(A\) elevados ao quadrado e autovetores de \(S\) são vetores vetores singulares direitos de \(A\)

Autovalores e valores singulares

Existe alguma relação entre autovalores e valores singulares?

\[ AA^\top = ?\]

Como \(A = U\Sigma V^\top\)

\[\begin{align} A A^\top &= U\Sigma V^\top (U\Sigma V^\top)^\top \\ &= U \Sigma \underbrace{V^\top V}_{I}\Sigma U^\top\\ &= U\Sigma^2 U^\top\\ &= \underbrace{ \begin{bmatrix} \vert & \ldots & \vert \\ u_1 & \ldots & u_r \\ \vert & \ldots & \vert \end{bmatrix}}_{Q} \underbrace{ \begin{bmatrix} \sigma_1^2 && \\ & \ddots & \\ && \sigma_r^2 \end{bmatrix}}_{\Lambda} \underbrace{\begin{bmatrix} - & u_1 & - \\ - & \vdots &- \\ - & u_r & - \end{bmatrix}}_{Q} \end{align}\]

Note

Autovalores de \(S = AA^\top\) são valores singulares de \(A\) elevados ao quadrado e autovetores de \(S\) são vetores vetores singulares esquerdos de \(A\)

Autovalores e valores singulares

\(V\) possui os autovetores de \(A^\top A\)
\(U\) possui os autovetores de \(AA^\top\)
O quadrado dos valores da diagonal de \(\Sigma\) são os autovalores de \(A^\top A\) e \(AA^\top\)

Decompondo A

Calcule os autovetores \(v\)’s de \(A^\top A\)
Faça \(\sigma_k = \sqrt{\lambda_k}\)
Então calcule:
\[ u_k = \frac{Av_k}{\sigma_k} \]

Note

Primeiro calcule a decomposição espectral de \(\overbrace{A^\top A}^{n\times n} = \overbrace{Q}^{n\times n} \overbrace{\Lambda}^{n\times n} \overbrace{Q^\top}^{n\times n} = V \Lambda V^\top\)

Observe que \(\Lambda = \begin{bmatrix}\sigma_1^2 &&&&& \\ & \ddots &&&& \\ && \sigma_r^2& &&&\\ &&& 0 &&\\ &&&& \ddots & \\ &&&&& 0 \end{bmatrix}\)

Observe também qu \(Av_i = \sigma_i u_i \Rightarrow u_i = \frac{Av_i}{\sigma_i}\) ou matricialmente \(U = AV\Sigma^{-1}\)

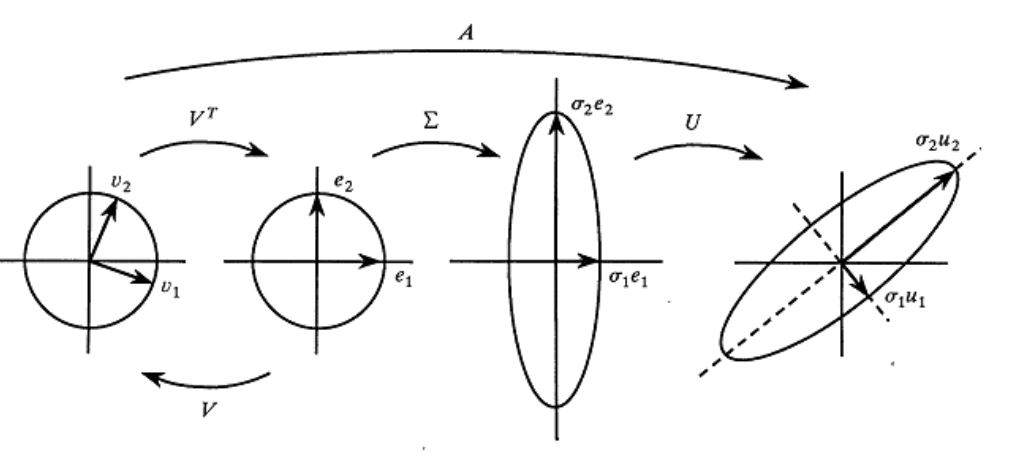
Geometria de SVD

Vamos começar por uma matriz de rotação \(R\):

\[R(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix} \]

\[R(\pi/4) = \begin{bmatrix} \cos(\pi/4) & -\sin(\pi/4)\\ \sin(\pi/4) & \cos(\pi/4) \end{bmatrix} \]

\[R(\pi/4) = \begin{bmatrix} 1/\sqrt{2} & -1/\sqrt{2}\\ 1/\sqrt{2}& 1/\sqrt{2} \end{bmatrix} \]

Geometria de SVD

Vamos começar por uma matriz de rotação \(R\): \[R(\pi/4)x = \begin{bmatrix} 1/\sqrt{2} & -1/\sqrt{2}\\ 1/\sqrt{2}& 1/\sqrt{2} \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = ? \]

Ex: \(x = \begin{bmatrix}3\\2\end{bmatrix} = 3\begin{bmatrix}1\\0\end{bmatrix}+ 2\begin{bmatrix}0\\1\end{bmatrix} = 3e_1 + 2e_2\)

\[Rx = c_1Re_1 + c_2Re_2 = 3Re_1 + 2Re_2\]

\[ Rx = 3 \begin{bmatrix} 1/\sqrt{2} & -1/\sqrt{2}\\ 1/\sqrt{2}& 1/\sqrt{2} \end{bmatrix}\begin{bmatrix} 1\\ 0 \end{bmatrix} + 2 \begin{bmatrix} 1/\sqrt{2} & -1/\sqrt{2}\\ 1/\sqrt{2}& 1/\sqrt{2} \end{bmatrix}\begin{bmatrix} 0\\ 1 \end{bmatrix} \]

\[ Rx = 3 \begin{bmatrix} 1/\sqrt{2} \\ 1/\sqrt{2} \end{bmatrix} + 2 \begin{bmatrix} -1/\sqrt{2}\\ 1/\sqrt{2} \end{bmatrix} \] ## Geometria de SVD

O que significa multiplicar um vetor \(v\) por \(A\)

\[A v = (U\Sigma V^\top)v = U \Sigma (V^\top v)\]

Note

\(V\) (\(V^\top\)) é uma matriz ortogonal. Produto de um vetor por uma matriz ortogonal pode ser vista como rotação ou reflexão. Lembrando que \(V^\top\) é a inversa de \(V\)

Observe que \(Ve_1 = v_1\) e \(Ve_2 = v_2\)

Observe também que \(V^\top v_1 = \begin{bmatrix}-&v_1^\top & - \\ - & v_2^\top & -\end{bmatrix}\begin{bmatrix}v_1\end{bmatrix} = \begin{bmatrix}1\\0\end{bmatrix}\). Lembrando que \(v_1\) é ortogonal a \(v_2\)

Geometria de SVD

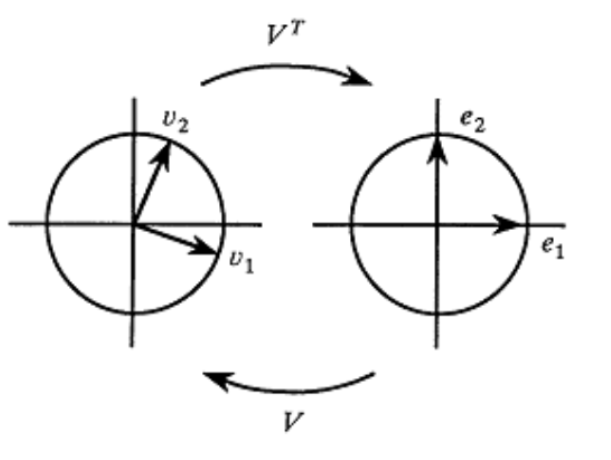
Note

um vetor \(v\) pode ser escrito como \(v = c_1v_1+c_2v_2 + \ldots\)

\(V^\top v = \begin{bmatrix}c_1\\c_2\end{bmatrix}\)

Geometria de SVD

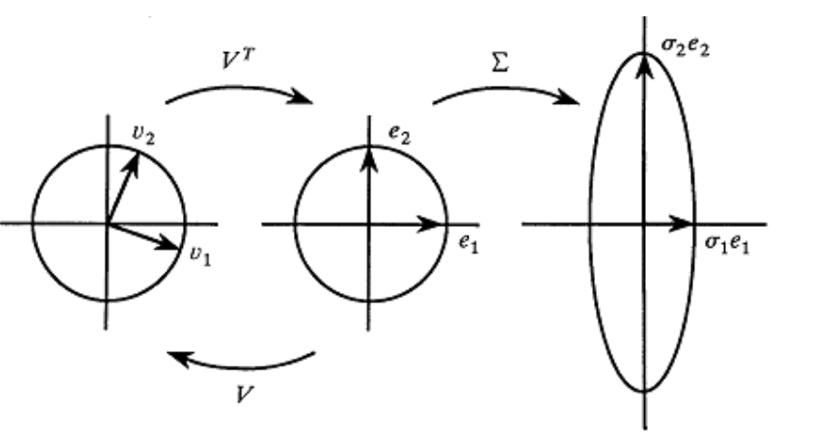
Agora vamos ver o que acontece quando usamos uma matriz de escala \(\Sigma\):

\[ \Sigma(\sigma_1, \sigma_2) = \begin{bmatrix} \sigma_1 & 0\\ 0 & \sigma_2 \end{bmatrix} \]

\[ \Sigma(2.0, 0.5)x = \begin{bmatrix} 2.0 & 0\\ 0 & 0.5 \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = \begin{bmatrix}2.0 x_1 \\ 0.5 x_2\end{bmatrix} \]

Geometria de SVD