Álgebra Linear Computacional
Aula 11: SVD e aproximação de matrizes
ramosh@dcc.ufmg.br
Créditos
Important
Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento
Objetivos de aprendizagem
- Entender fundamentos da aplicação do SVD para sistemas de recomendação
- Calcular representação latente de usuários e filmes
- Saber fazer a compressão de imagens usando SVD
- Entender a relação entre qualidade da imagem comprimida e seu espectro (conjunto de valores singulares)
- Saber encontrar aproximação de matrizes (ou de elementos específicos) usando SVD truncado
- Conhecer e entender o Teorema de Eckart-Young
Referências adicionais
\(AV = U\Sigma\)
\[A\begin{bmatrix}\vert & \vert & \ldots & \vert \\ v_1 & v_2 & \ldots & v_r\\\vert & \vert & \ldots & \vert \end{bmatrix} = \begin{bmatrix}\vert & \vert & \ldots & \vert \\ u_1 & u_2 & \ldots & u_r\\\vert & \vert & \ldots & \vert \end{bmatrix}\begin{bmatrix}\sigma_1 & & \\ &\ddots&\\&&\sigma_r\end{bmatrix} \]
Note
Essas dimensões correspondem ao SVD reduzido
Precisamos transformar \(U\) e \(V\) em matrizes quadradas
Tornando \(V\) quadrada
Se o espaço coluna \(C(A)\) tem dimensão \(r\), existem \(r\) vetores \(\sigma_iu_i\) independentes que podem ser escritos como \(Av_i\)
Sabemos ainda que o espaço nulo \(N(A)\) tem dimensão \(n-r\)
Logo, existem \(n-r\) vetores \(v_j\) independentes tais que \(Av_j=0\)
Esses vetores são orgotonais a \(v_1,\ldots,v_r\), concatenando-os a \(V\),
\[ A_{m\times n} \underbrace{ \begin{bmatrix} \vert & \ldots & \vert & & \vert& \ldots &\vert\\ v_1 &\ldots & v_r && v_{r+1} & \ldots & v_n\\ \vert & \ldots & \vert & & \vert& \ldots &\vert \end{bmatrix}}_{n\times n} = \underbrace{ \begin{bmatrix} \vert & \ldots & \vert\\ u_1 & \ldots & u_r\\ \vert & \ldots & \vert\\ \end{bmatrix}}_{m\times r} \underbrace{ \begin{bmatrix} \sigma_1 &\ldots & 0 && 0 &\ldots & 0\\ \vdots &\ddots & \vdots && \vdots &\ddots & \vdots\\ 0 &\ldots & \sigma_r && 0 &\ldots & 0\\ \end{bmatrix}}_{r\times n} \]
Tornando \(U\) quadrada
Como os vetores \(u_i\) estão no \(\mathbb R^m\), existem \(m-r\) vetores independentes \(u_j\) ortogonais a \(u_1, \ldots, u_r\). Logo, podemos concatená-los a \(U\), desde que sejam adicionadas \(m-r\) linhas nulas em \(\Sigma\):
\[ A_{m\times n} \underbrace{ \begin{bmatrix} \vert & \ldots & \vert & & \vert& \ldots &\vert\\ v_1 &\ldots & v_r && v_{r+1} & \ldots & v_n\\ \vert & \ldots & \vert & & \vert& \ldots &\vert \end{bmatrix}}_{n\times n} = \underbrace{ \begin{bmatrix} \vert & \ldots & \vert & & \vert& \ldots &\vert\\ u_1 & \ldots & u_r && u_{r+1} & \ldots & u_m\\ \vert & \ldots & \vert & & \vert& \ldots &\vert\\ \end{bmatrix}}_{m\times m} \underbrace{ \begin{bmatrix} \sigma_1 &\ldots & 0 && 0 &\ldots & 0\\ \vdots &\ddots & \vdots && \vdots &\ddots & \vdots\\ 0 &\ldots & \sigma_r && 0 &\ldots & 0\\ \\ 0 &\ldots & 0 && 0 &\ldots & 0\\ \vdots &\ddots & \vdots && \vdots &\ddots & \vdots\\ 0 &\ldots & 0 && 0 &\ldots & 0\\ \end{bmatrix}}_{m\times n} \]
Note
Essas dimensões correspondem ao SVD completo
Do SVD completo ao reduzido
SVD Completo
\[\underbrace{A}_{m\times n} = \underbrace{U}_{m\times m} \underbrace{\Sigma}_{m\times n}\underbrace{V^\top}_{n\times n}\]
Como apenas os \(r\) primeiros termos da diagonal de \(\Sigma\) são não-nulos, podemos tomar essa submatriz descartando as colunas \(r+1,\ldots,m\) de \(U\) e as linhas \(r+1,\ldots,n\) de \(V^\top\). O resultado, denotado pelas mesmas letras é
SVD Reduzido
\[\underbrace{A}_{m\times n} = \underbrace{U}_{m\times r} \underbrace{\Sigma}_{r\times r}\underbrace{V^\top}_{r\times n}\]
Exemplo de uma matriz tall-thin
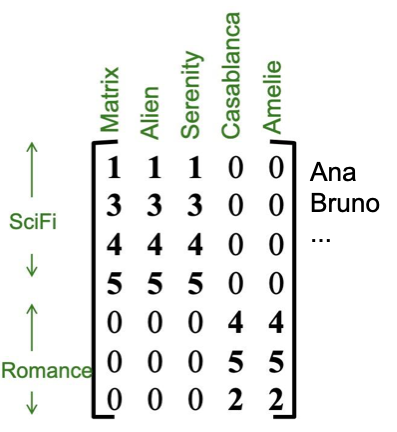
Tall-thin matrix
Aprendendo sobre espaço latente

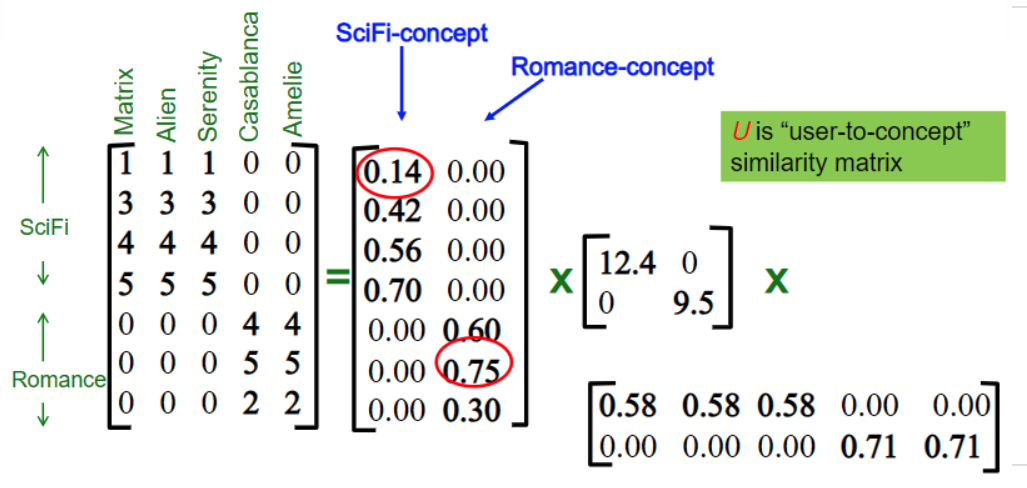
Usuário e conceito
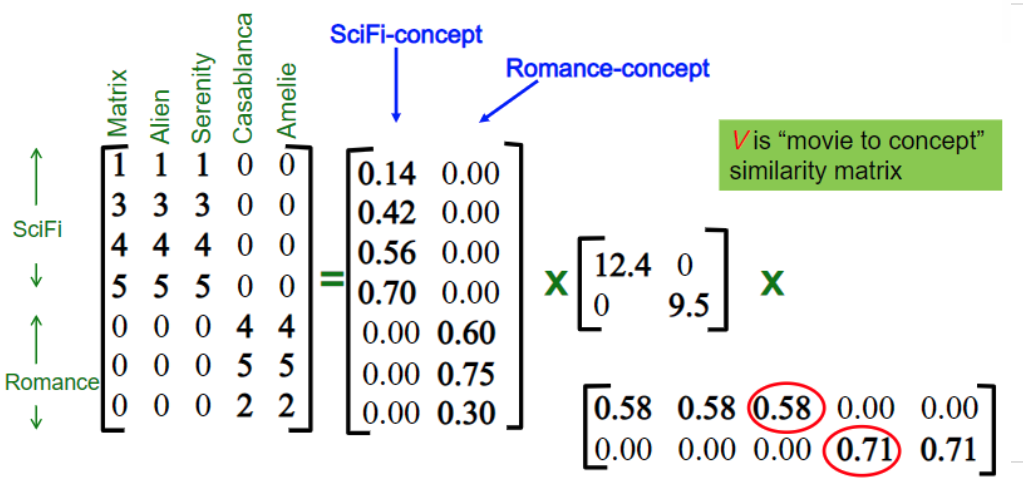
Filme e conceito
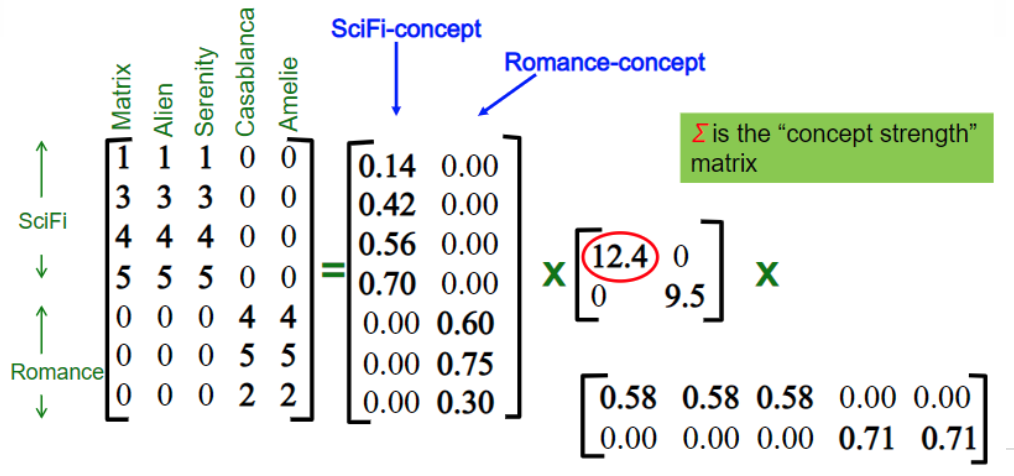
Peso de um conceito
Exemplo um pouco mais real
Note que existem usuários que vão assistir filmes de vários tipos (isso pode ser apenas ruído) 
Exemplo um pouco mais real

Um sistema de recomendação simples
- Temos \(k\) perfis de usuários
- Cada usuário será o resultado da combinação linear desses perfis (comédia, drama, ação)
- A matrix “verdadeira” então terá posto \(k\)!
- Pergunta
- Como recomendar um filme para um determinado usuário?
Um sistema de recomendação simples

Um sistema de recomendação simples
Como estamos supondo termos \(k=2\) perfis

Um sistema de recomendação simples
Ao realizar a multiplicação (após remover o menor valor singular)

Compressão de imagens
\(\approx 80\%\) da internet é imagem!

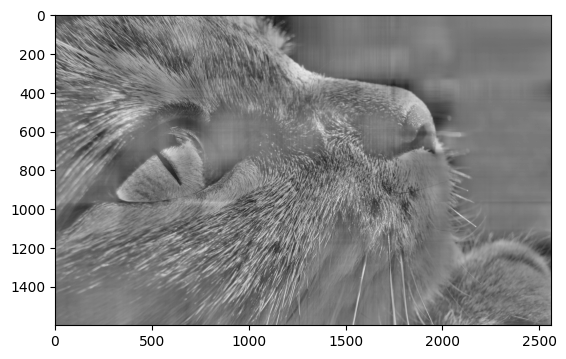
Compressão de imagens
Dimensões: (2560 x 1600) Número de bytes: 4.096.000 (imagem em tons de cinza - 1 byte por pixel)

Compressão de imagens
Podemos tentar aproximar a matriz \(A\) que representa a imagem por \(A_k\)
\[ A_k = \sigma_1 u_1 v_1^\top + \ldots + \sigma_k u_k v_k^\top\]
Compressão de imagens
U, sigma, Vt = np.linalg.svd(img_gray)
U.shape: 1600 x 1600
Vt.shape: 2560 x 2560
sigma.shape: 1600 x 1600 (sendo apenas 1600 valores diferentes de zero)
Compressão de imagens
- A primeira aproximação seria \(A_1\)

Compressão de imagens
Como saber se ficou bom?
\[ RMSE = \sqrt{\frac{1}{MN}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}\left(I_1(m,n)-I2(m,n)\right)^2}\]
\[RMSE(AK_1) = 131361.669\]
\[RMSE(AK_5) = 80013.826\]
\[RMSE(AK_{20}) = 56411.098\]
\[ RSME(AK_{100}) = 21429.215\]
Como ficaram as imagens?





Como ficaram os erros (visualmente)?



Até quando precisamos ir?

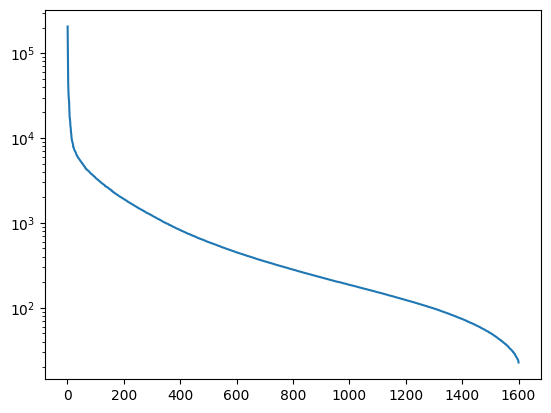
Até quando precisamos ir?
Regra do dedão: cortar de maneira a mantar entre 80-90% da “energia”
\[t = \frac{\sum_{i=1}^k \sigma_i^2}{\sum_{i=1}^n \sigma_i^2} \]

Energia
Resultados com \(A_{400}\)


\[RMSE(A_{400}) = 10969.759\]
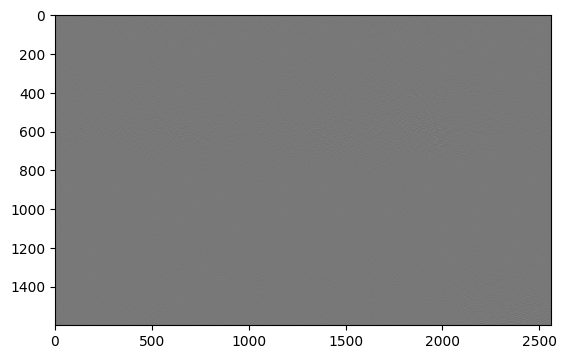
Qual foi a taxa de compressão?
\[T_x = (400 * 1600 + 400 + 400*2560)/(1600*2560)\] \[T_x = 40,63\%\]
Razão de compressão: \((1600*2560)/(400 * 1600 + 400 + 400*2560) = 2,46\) vezes
Parece pouco?
Aproximação da matriz
É possível encontrar uma matriz \(B\) com posto \(k\) que seja mais próxima de \(A\) e que não seja \(A_k\)?
Aproximação de matriz
Eckart-Young: Suponha \(B\) uma matriz de posto \(k\). Então \(B\) será uma aproximação no máximo tão boa quanto
\[A_k = \sigma_1u_1v_1^\top + \ldots + \sigma_ku_kv_k^\top \]
Aproximação de matriz
Se \(B\) tem posto \(k\), então
\[ \Vert A - B \Vert \ge \Vert A - A_k \Vert\]
Norma de Frobenius:
\[ \Vert A \Vert_F = \sqrt{\vert a_{11}\vert^2 + \vert a_{12}\vert^2 +\ldots + \vert a_{mn}\vert^2}\]
Note
\(\Vert M \Vert_2\) é o maior valor singular \(\sigma_1\)
Relação entre Frobenius e norma-2: \[\Vert A\Vert_F \ge \Vert A\Vert_2\]
