Álgebra Linear Computacional

Aula 14: Removendo Viés com PCA

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento

Objetivos de aprendizagem

1. Conhecer representação de palavras por vetores one-hot e por embeddings, assim comom vantagens e desvantagens
2. Entender como usar a similaridade de cosseno para resolver analogias com word embeddings
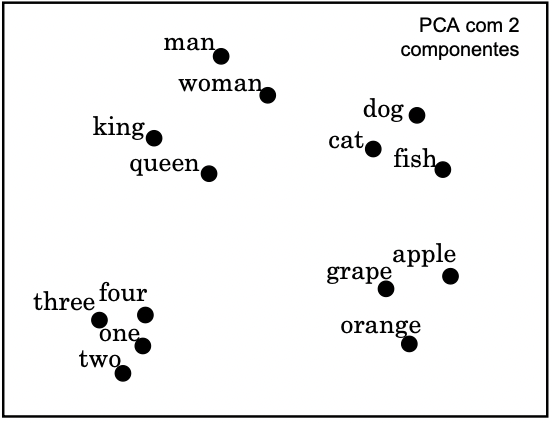
3. Entender o significado da 1a. Componente Principal do PCA sobre pares de word embeddings
4. Entender como projeções e distâncias podem ser medidas de viés
5. Saber realizar os passos de neutralização e equalização para remover viés

Refe

rências Adicionais {.scrollable} - Embedding Projector

Artigo: Bolukbasi, T., Chang, K. W., Zou, J. Y., Saligrama, V., & Kalai, A. T. (2016). Man is to computer programmer as woman is to homemaker? debiasing word embeddings. Advances in neural information processing systems, 29, 4349-4357.

Código

Motivação

Muitas aplicações recebem como entrada um conjunto de palavras

Motivação

Muitas aplicações recebem como entrada um conjunto de palavras

Como representar as palavras?

Opção 1: usando “one hot” vectors Cada vetor tem o tamanho do vocabulário e apenas uma entrada não-nula, igual a 1

Como representar as palavras?

Opção 1: usando “one hot” vectors

• Problemas:
  • Embora vetores possam ser representados com estruturas esparsas, modelos que usam essas entradas têm número MUITO grande de parâmetros
  • Não são capazes de capturar similaridade entre palavras

Como representar as palavras?

Opção 1: usando “one hot” vectors

• Similaridade de cosseno entre \(u\) e \(v\): \[\cos(u,v) = \frac{u\cdot v}{\Vert u\Vert \Vert v\Vert} \]

Vetores similares são úteis, p. ex., para auto-completar frases mesmo que sequência de palavras nunca tenha sido vistas

“Eu gostaria de tomar um suco de ________”

[laranja] [limão] [cupuaçú]

Como representar palavras?

Opção 2: usando representações densas (conhecidas como “word vectors”, “word embeddings”, “word representations”)

• Métodos usam palavras que aparecem ao redor (no contexto) de uma palavra \(w\) para obter os embeddings
• Existem métodos eficientes para obter embeddings no \(\mathbb R^d\) a partir de corpus contendo BILHÕES de palavras
  • Dimensão \(d\) costuma variar de 25 a 1000

Word Embeddings

Analogias

Homem está para mulher assim como Rei está para ? \(e_{man} \rightarrow e_{woman}\) assim como \(e_{king} \rightarrow e_{?}\)

Como usar os embeddings para resolver essa questão?

\(e_{man} - e_{woman} \approxeq e_{king} - e_{?}\)

\(e_{man} - e_{woman} = \begin{bmatrix}-2\\ -0.01\\0.01\\ 0.08\end{bmatrix}\)

\(e_{?} \approxeq e_{king} - (e_{man} -e_{woman}) = \begin{bmatrix}-0.95\\ 0.93\\0.70\\ 0.02\end{bmatrix} - \begin{bmatrix}-2\\ -0.01\\0.01\\ 0.08\end{bmatrix}\)

\(e_{?} = \begin{bmatrix}1.05\\0.94\\0.69\\-0.06\end{bmatrix}\)

Analogias

\(e_{?} \approxeq e_{king} - (e_{man} -e_{woman})\)

Encontre a palavra \(w\colon \text{arg}\max_w sim(e_w, e_{king} - e_{man} + e_{woman})\)

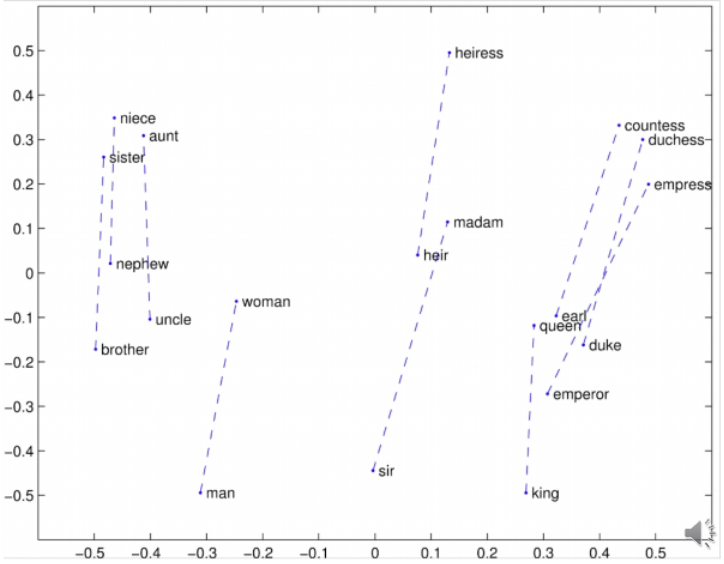
Exemplos semânticos

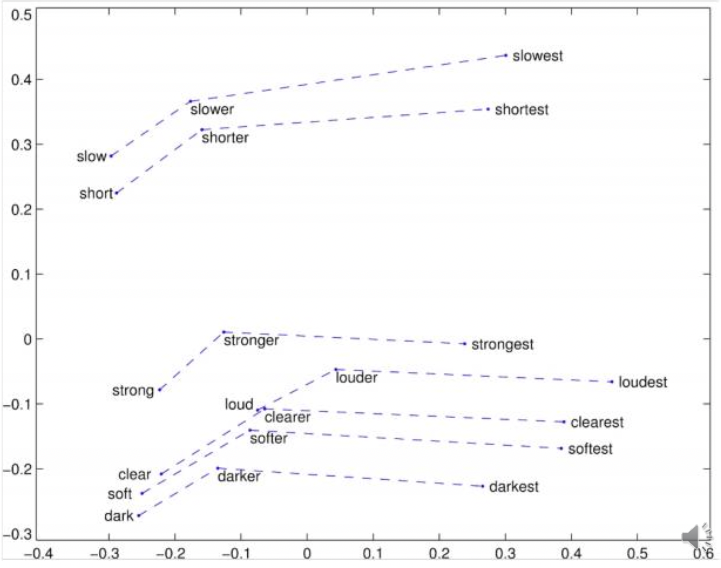
Exemplos sintáticos

Problema do viés

• Algoritmos baseados em AI são cada vez mais usados para tomar decisões muito importantes
• Por vezes queremos nos certificar de que são livres de viéses (p. ex., gênero, etnia)
• Veremos algumas ideias para remover ou reduzir viés

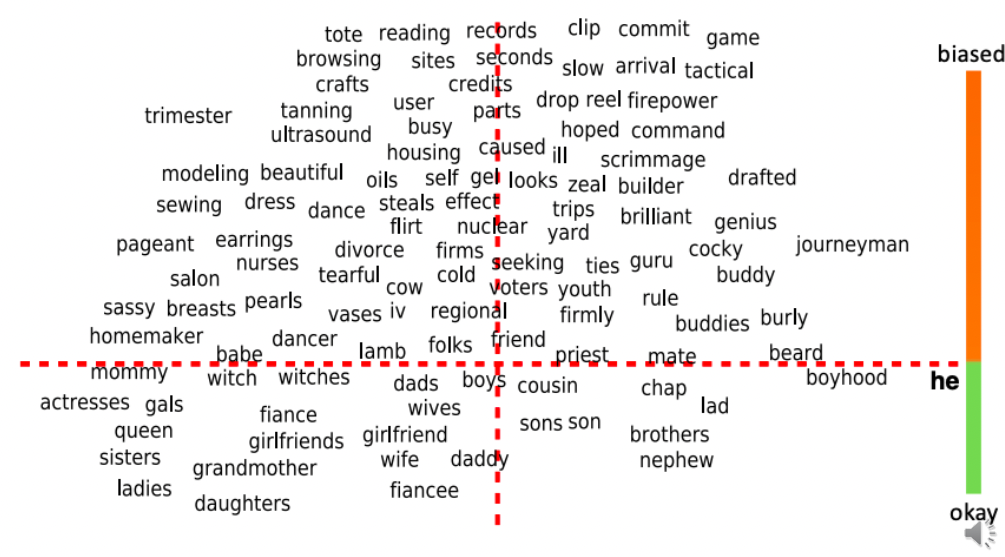
Viés em word embeddings

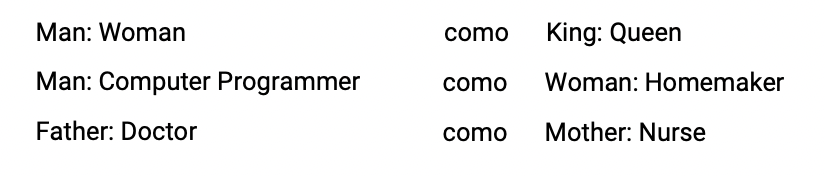
• Word embeddings podem refletir viéses de gênero, etnia, idade e orientação sexual presentes no texto usado para treiná-los
• Note que algoritmos de ML influenciam admissões em faculdades, matching de candidatos a empregos, empréstimos, guidelines usados para sentenças de prisão

Viés em word embeddings

Removendo viés em word embedding

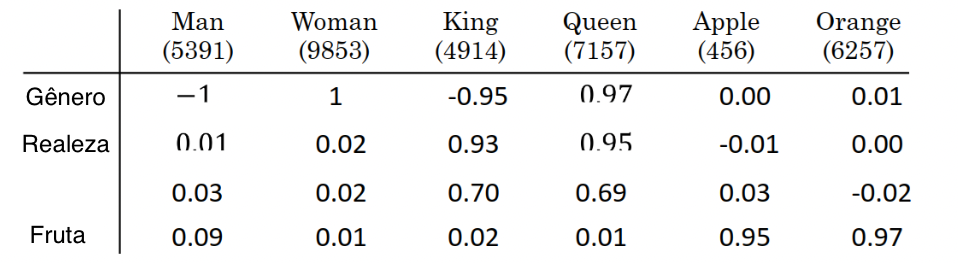
1. Identifique a direção do viés usando palavras definicionais:

\(\longleftarrow \text{ média }\begin{cases}e_{he}-e_{she}\\e_{male} - e_{female}\\ \ldots\end{cases}\)

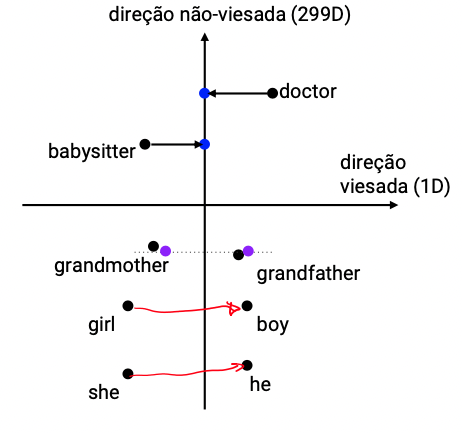
2. Neutralize: para cada palavra neutra de gênero projete na direção não-viesada para se livrar do viés
3. Equalize os pares de palavras definicionais para que palavras neutras tenham mesma distância dos pares

Removendo viés em word embedding

Identificação do viés: Na prática, a direção do viés é calculada usando-se PCA, em vez da média

Passo de neutralização:

• Palavras definicionais capturam gênero intrinsecamente: mãe, pai, irmão, irmã
• Outras palavras são neutras de gênero: doctor, babysitter
  • Queremos que sejam neutras de gênero (e, de forma geral, de etnia, etc)

Passo de equalização:

• Queremos que única diferença entre palavras definicionais seja gênero. Caso contrário, diferença entre babysitter e grandmother será > diferença entre babysitter e grandfather.
• Para isso, é preciso que (i) as representações na direção não-viesada destes pares seja exatamente igual, e que (ii) eles sejam simétricos na direção viesada.

Como decidir que palavras devem ser neutralizadas? Autores treinaram classificador para identificar quais palavras são definicionais (em inglês, são uma minoria).

Quais pares equalizar? Em geral, podem ser escolhidos a mão

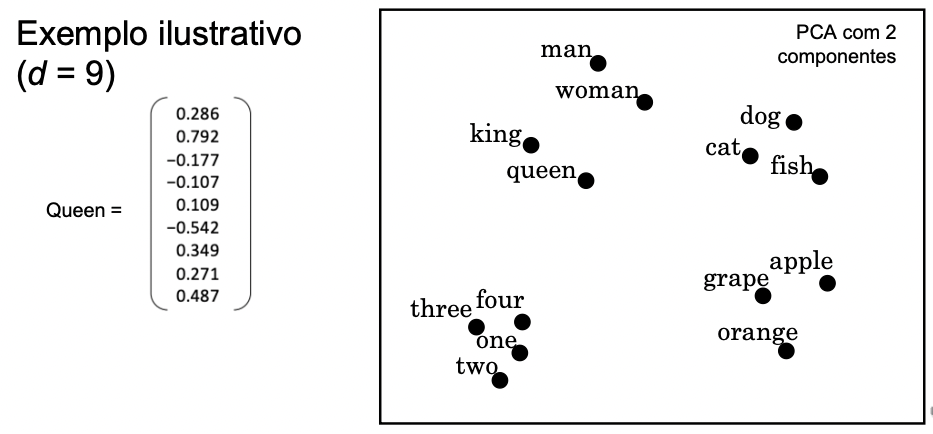
Passo 1: o subespaço gênero

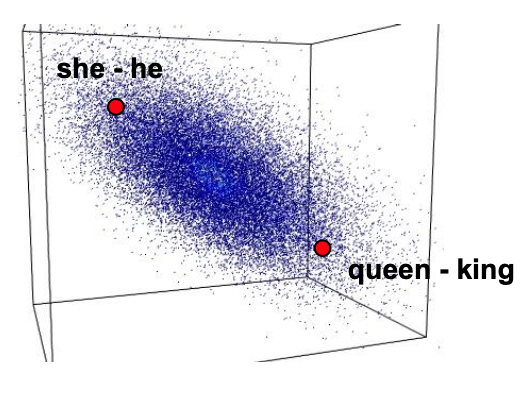
Os vetores diferença she - he, queen - king, etc não são exatamente iguais

Como encontrar subespaço que codifica gênero?

• Uma ideia é usar a média das diferenças (1D, ou seja, uma reta)
• Melhor ainda é usar o PCA para encontrar as componentes principais

Uma nuvem de pontos

Rodando eixos com cuidado

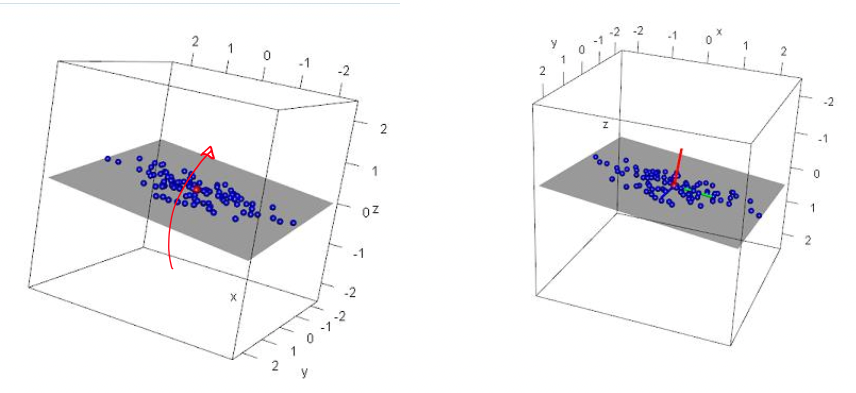
PCA

• Se os embeddings estão no \(\mathbb R^d\), a primeira componente principal é um vetor \(g\) no \(\mathbb R^d\)
• Sejam \(D_1, \ldots, D_n\) pares definicionais P. ex.: \(D_i =\) (‘boy’, ‘girl’)
• Para obter vetor \(g\):
  • Obter matriz \(X_{n \times d}\) das diferenças dos embeddings
  • Obter matriz \(M\) centralizando matrix \(X\)
  • Calcular matriz de covariância \(M^\top M\)
  • Obter \(g\), o 1o autovetor de \(M^\top M\)

Subespaço não-viesado

Agora que definimos o subespaço gênero, \[ \text{a reta } B = \{ag\colon a\in \mathbb R\}\]

Podemos definir o subespaço não-viesado ortogonal a ele:

\[S_{\perp B} = \{x \in \mathbb R^d\colon g^\top x = 0\}\] \[S_{\perp B}\colon g_1x_1 + g_2x_2 + \ldots + g_nx_n = 0\]

Passo 2: neutralização

Neutralizar um embedding \(x\) equivale a

• Projetar no subespaço não-viesado ou
• Remover a componente viesada:

\[ x - x_B\]

\[ x \leftarrow x - (x\cdot g) g\]

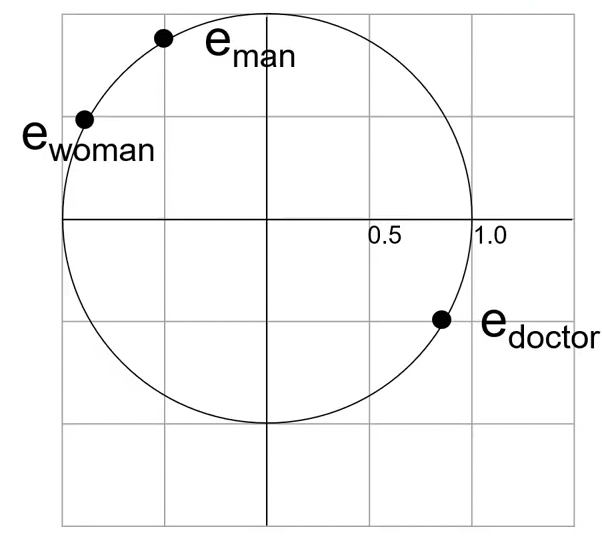
Neutralização (exemplo)

\(e_{man} =(-0.50,0.87)\)

\(e_{woman}=(-0.87,0.50)\)

\(e_{doctor} = (0.87,-0.50)\)

Neutralize \(e_{doctor}\)

\(g = e_{man} - e_{woman}\)

\(g = (0.37, 0.37)\)

Queremos que ele seja unitário: \[ g = \frac{g}{\Vert g\Vert}_2 = (0.71, 0.71)\]

\[\begin{align} e_B &= (e_{doctor}\cdot g)g\\ &= (0.87 \times 0.71 - 0.50 \times 0.71)g\\ &= 0.26(0.71, 0.71)\\ &= (0.18, 0.18) \end{align}\]

\[\begin{align} e_{doctor} &= e_{doctor} - e_B \\ &= (0.87, -0.50) - (0.18, 0.18) \\ &= (0.69, -0.69) \end{align}\]

\(e_{doctor} = \frac{e_{doctor}}{\Vert e_{doctor}\Vert_2} = (0.71, -0.71)\)

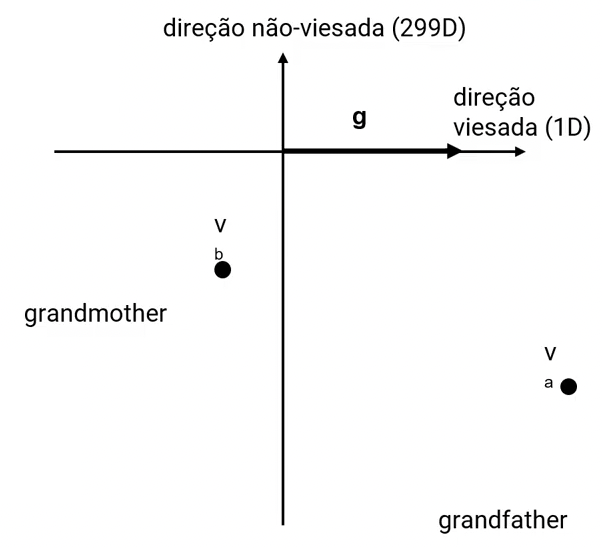
Passo 3: equalização

Um par definicional \((v_a,v_b)\) deve ter a mesma distância do plano não-viesado:

• Calcula média \(\mu = (va+vb)/2\)
• Remove viés \(y = \mu - \mu B\)
• Calcula componente viés \(z = \sqrt{1-\Vert y\Vert^2}\) de forma que \(\Vert y-zg\Vert = 1\)
• Adiciona viés \(z\) e \(-z\) para obter \(v_a = y + zg\) e \(v_b = y - zg\) embeddings neutralizados

Resumo

Word embeddings são representações densas de palavras usadas em tarefas de ML

• Embeddings podem conter viéses do conjunto de treinamento
• Vimos uma maneira de remover viés usando PCA
  • Neutralizando palavras “neutras”
  • Equalizando palavras definicionais