Álgebra Linear Computacional
Aula 15: Regressão Linear
Créditos
Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento
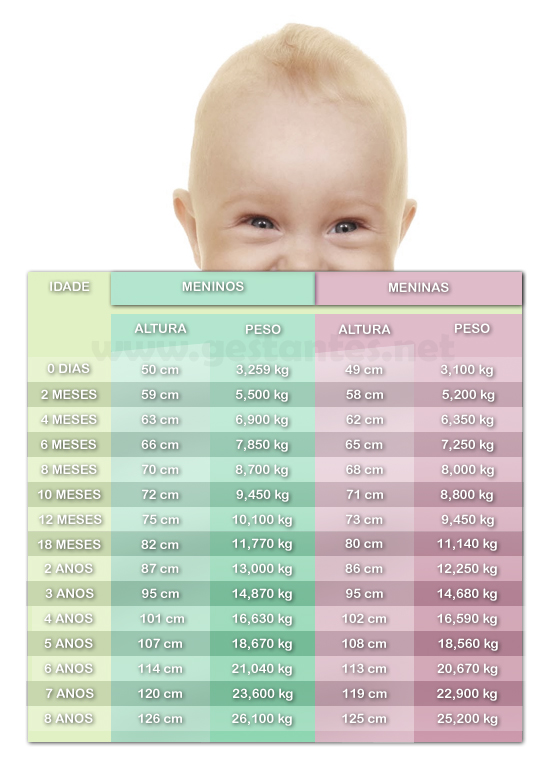
Altura dos Bebês
Existe uma relação entre o tamanho e a idade de uma criança?
Se sim, como essa relação se comporta?
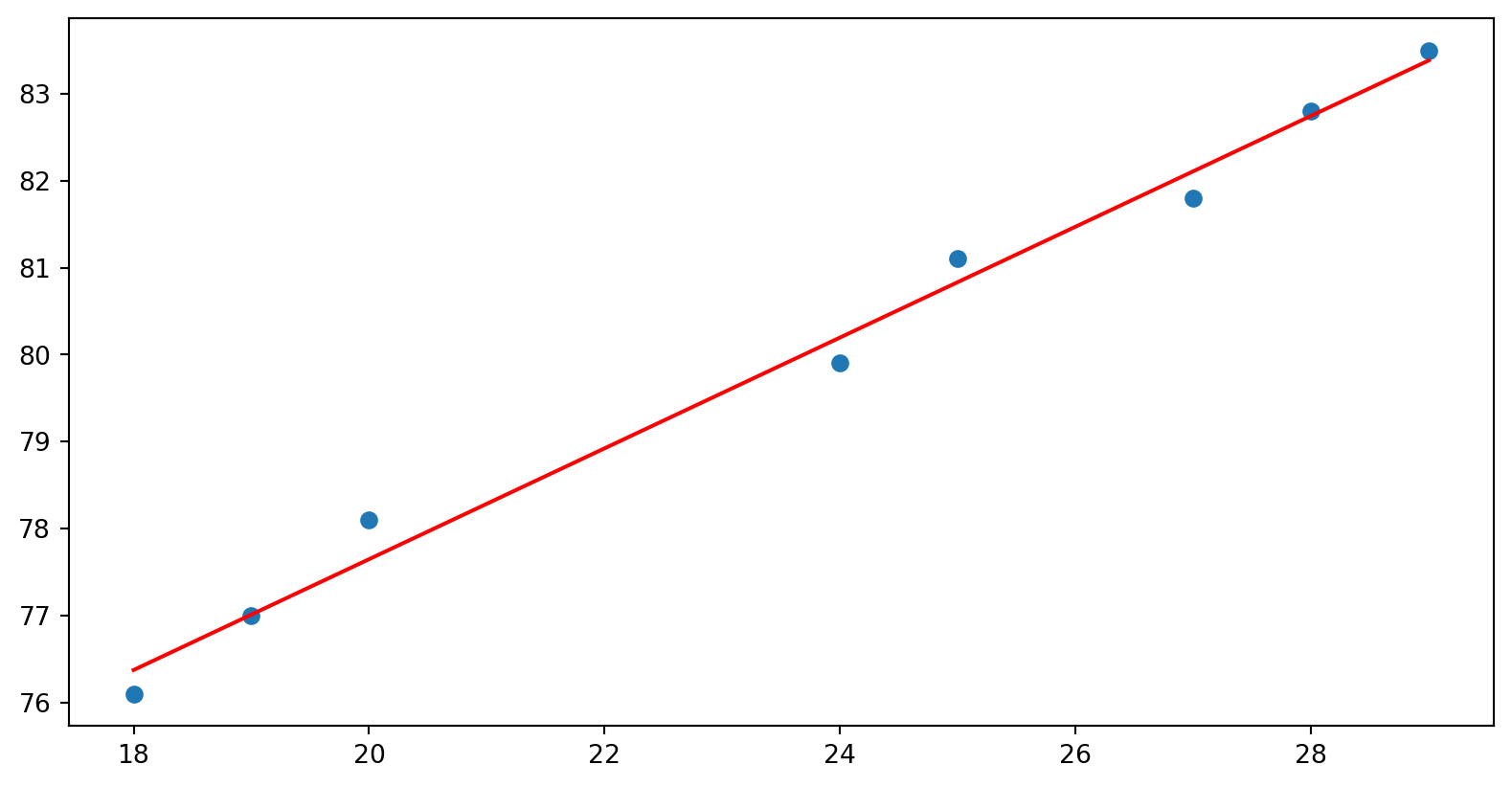
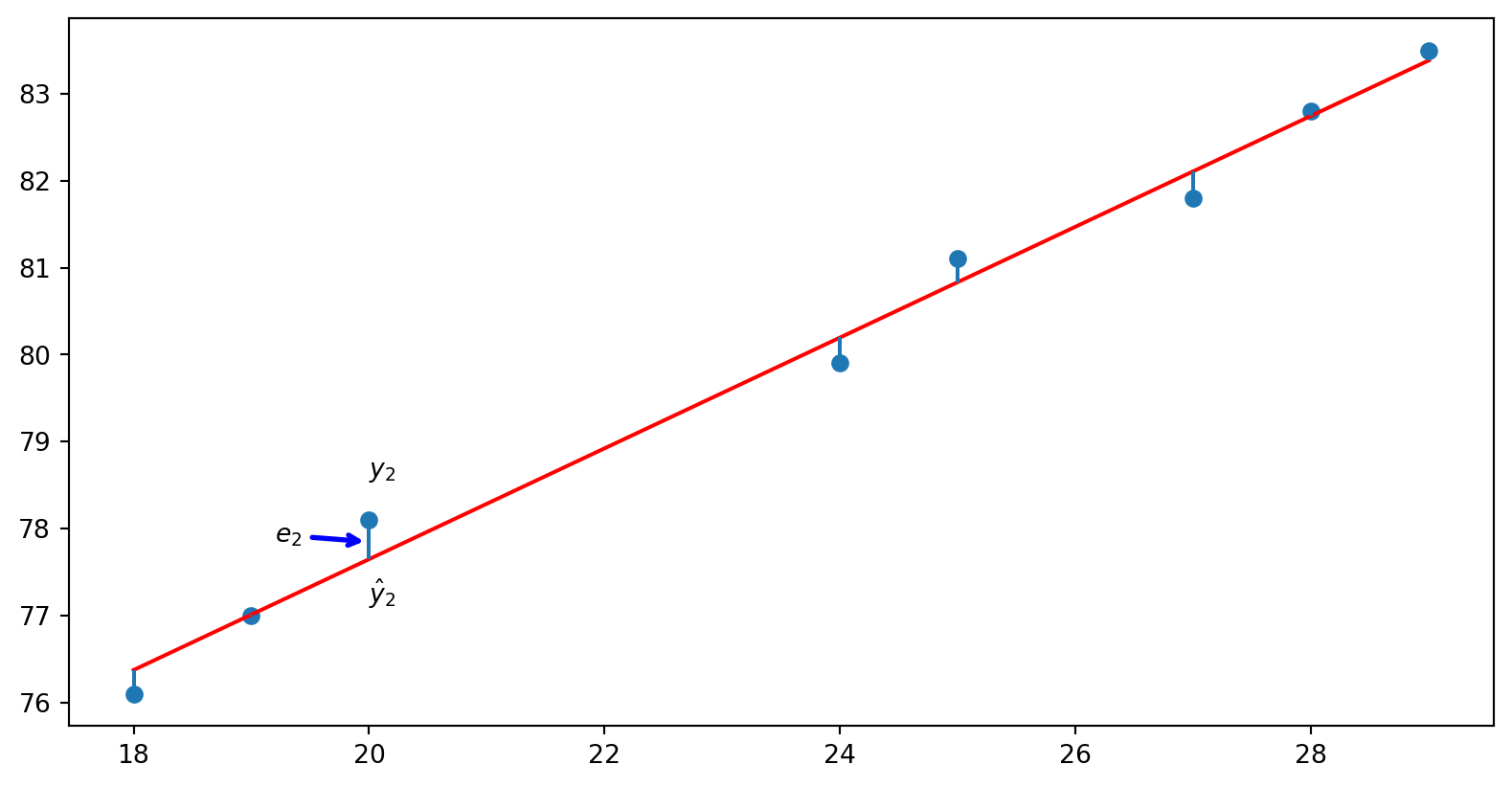
Vamos analisar os dados
18
76.1
19
77
20
78.1
24
79.9
25
81.1
27
81.8
28
82.8
29
83.5
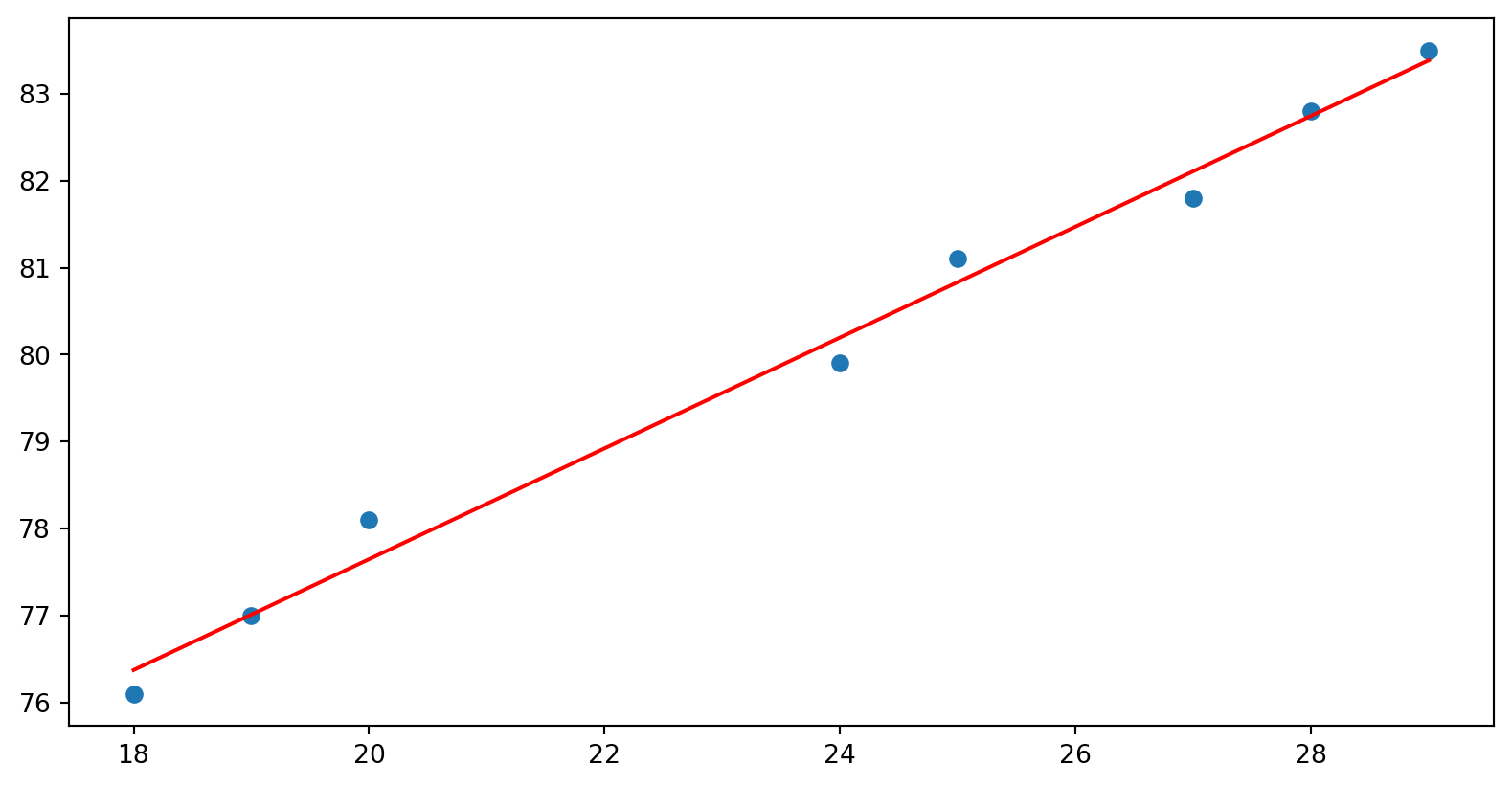
Vamos analisar os dados
18
76.1
19
77
20
78.1
24
79.9
25
81.1
27
81.8
28
82.8
29
83.5
Code
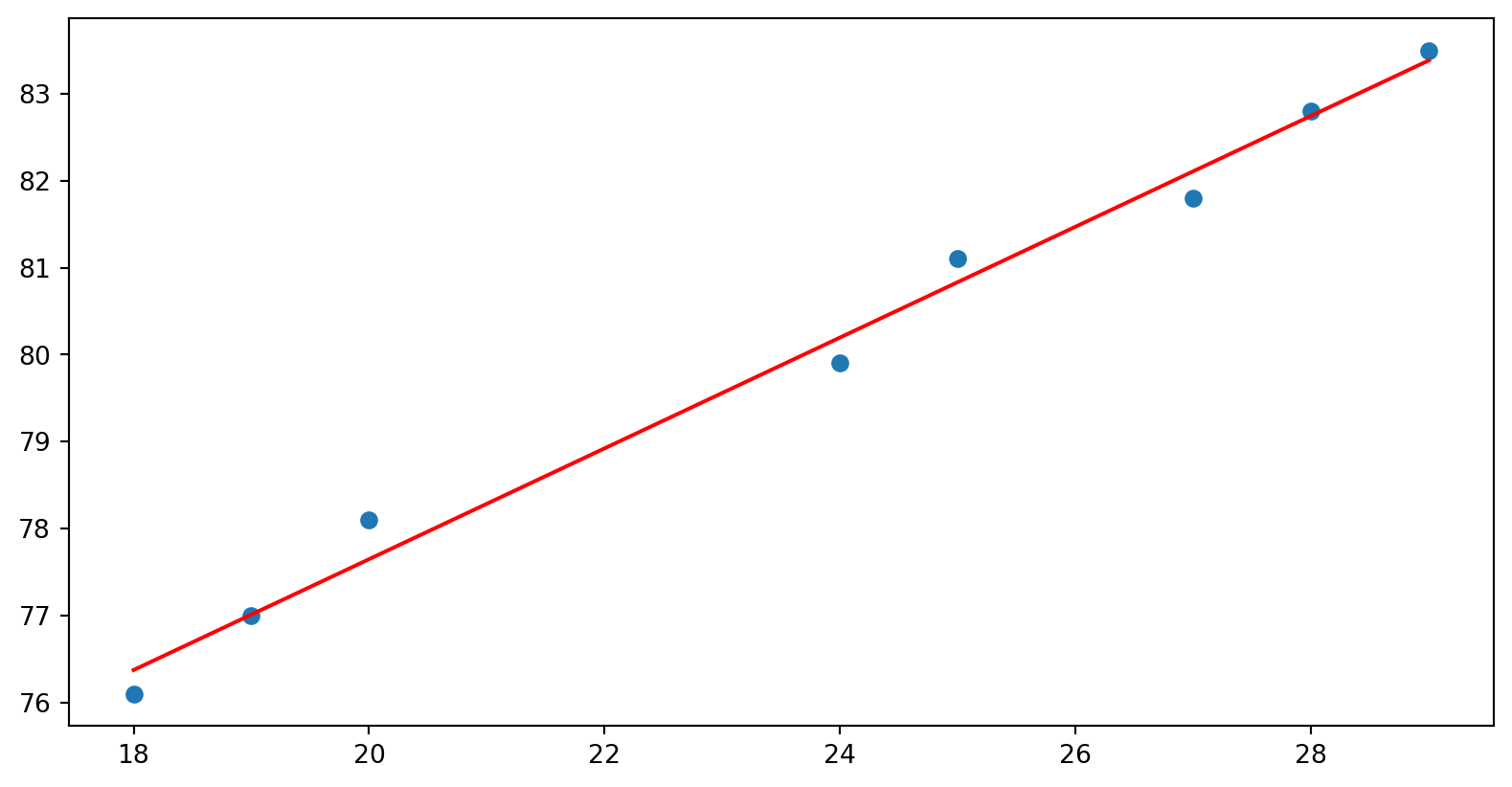
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression= np.array([18 ,19 ,20 ,24 ,25 ,27 ,28 ,29 ]).reshape(- 1 , 1 )= np.array([76.1 , 77 , 78.1 , 79.9 , 81.1 , 81.8 , 82.8 , 83.5 ]).reshape(- 1 , 1 )= LinearRegression()= "red" )
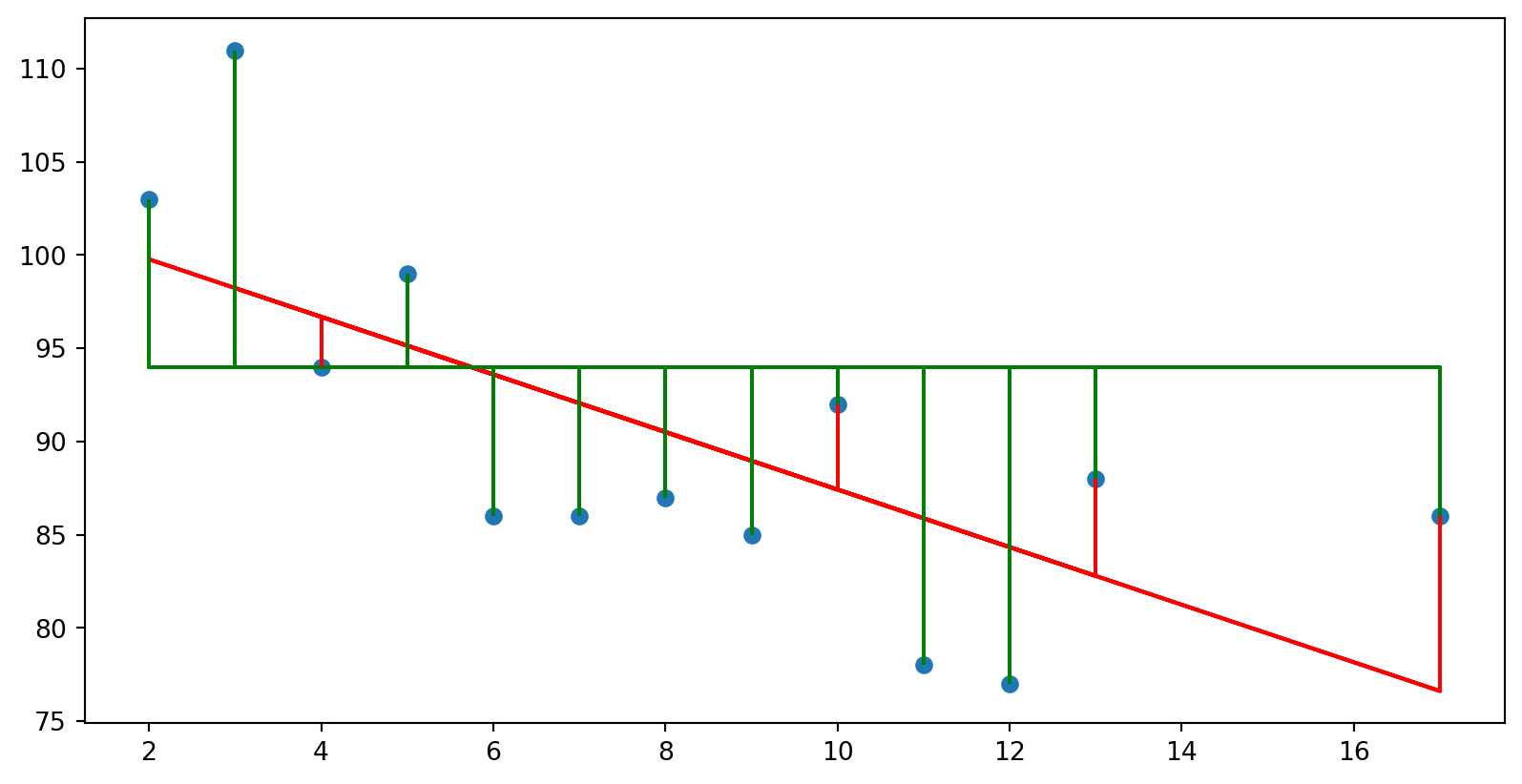
Critério de escolha da reta
Buscar a reta que minimiza a soma de todos os resíduos
Vamos calcular \(\beta_0\) e \(\beta_1\) que minimize a soma dos quadrados dos resíduos
\[E = \sum_{i=1}^n (y_i -\beta_1x_0 - \beta_0)^2\]
Code
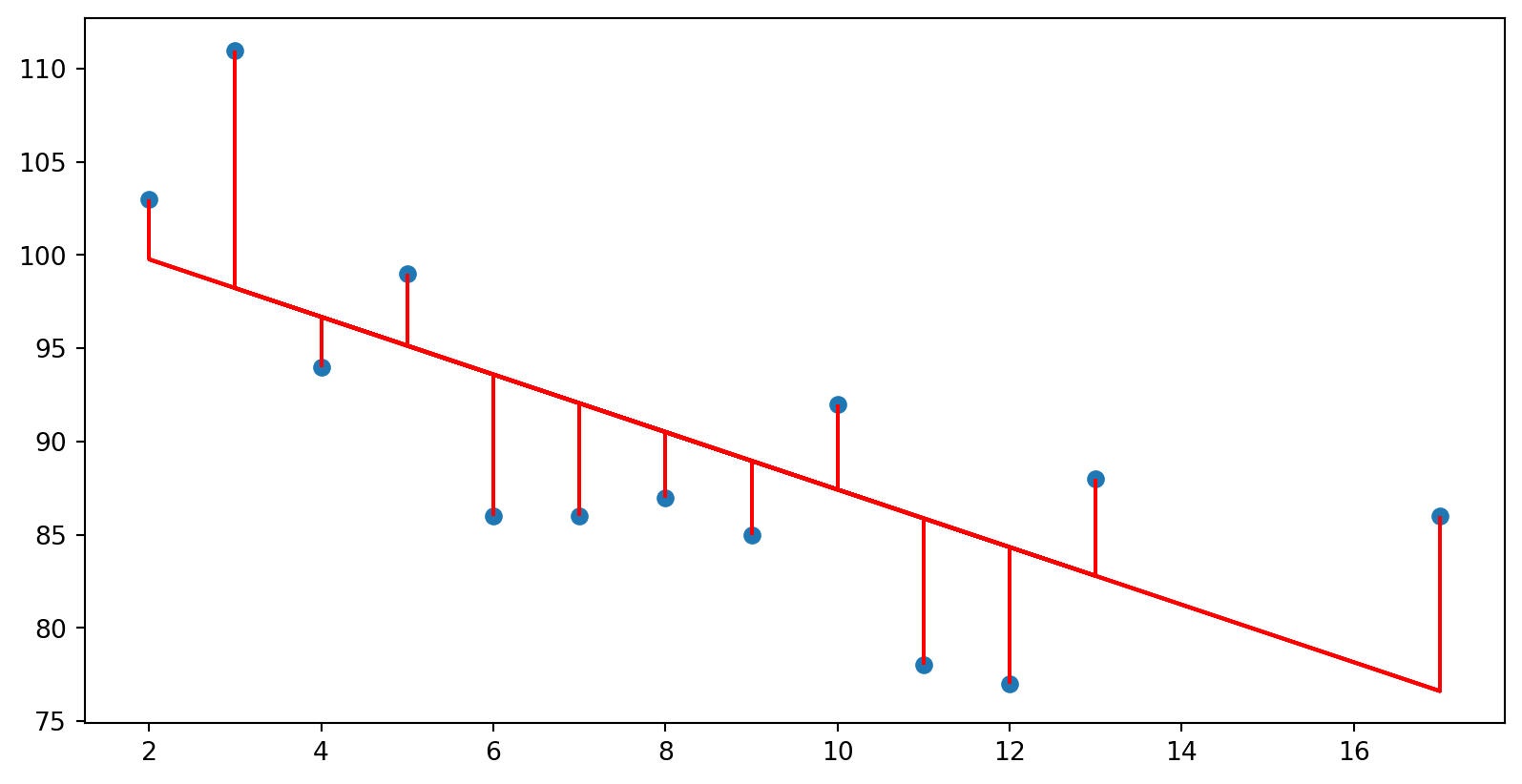
import numpy as npimport itertools import matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegression= np.array([5 ,7 ,8 ,13 ,3 ,17 ,2 ,10 ,4 ,11 ,12 ,9 ,6 ]).reshape((- 1 ,1 ))= np.array([99 ,86 ,87 ,88 ,111 ,86 ,103 ,92 ,94 ,78 ,77 ,85 ,86 ]).reshape((- 1 ,1 ))= LinearRegression()= model.predict(x)= "red" )for i in range (13 ):= "red" )
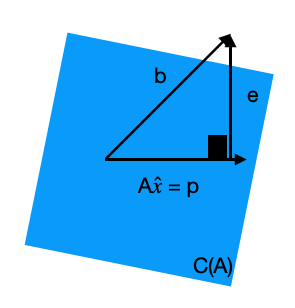
Solução da equação normal
\[ A^\top A \hat{x} = A^\top b\]
Sejam
\[A = \begin{bmatrix}1 & x_1\\ \vdots & \vdots\\ 1 & x_n\end{bmatrix} \]
e \[ b = \begin{bmatrix}y_1 \\ \vdots\\ y_n\end{bmatrix}\]
Vamos analisar a matriz \(A^\top A\)
\[\begin{align}
A^\top A &=
\begin{bmatrix}
1 & 1 & \ldots & 1\\
x_1& x_2& \ldots & x_n
\end{bmatrix}
\begin{bmatrix}
1 & x_1\\
1 & x_2 \\
\vdots & \vdots \\
1 & x_n
\end{bmatrix}\\
&=
\begin{bmatrix}
\sum_{i=1}^n 1 & \sum_{i=1}^n x_i \\
\sum_{i=1}^n x_i & \sum_{i=1}^n x_i^2
\end{bmatrix}\\
&=\begin{bmatrix}
n & \sum_{i=1}^n x_i \\
\sum_{i=1}^n x_i & \sum_{i=1}^n x_i^2
\end{bmatrix}
\end{align}\]
Agora vamos analisar a matriz \(A^\top b\) \[\begin{align}
A^\top b &=
\begin{bmatrix}
1 & 1 & \ldots & 1\\
x_1& x_2& \ldots & x_n
\end{bmatrix}
\begin{bmatrix}
y_1 \\ \vdots\\ y_n
\end{bmatrix}\\
&=
\begin{bmatrix}
\sum_{i=1}^n y_i \\
\sum_{i=1}^n x_iy_i
\end{bmatrix}
\end{align}\]
Como solucionar \(A^\top A \hat{x} = A^\top b\) para \(\hat{x}\) ?
Método 1:
\[\begin{align}
A^\top A\hat{x} &= A^\top b \\
(A^\top A)^{-1}A^\top A\hat{x} &= (A^\top A)^{-1}A^\top b\\
\hat{x} &= (A^\top A)^{-1}A^\top b
\end{align}\]
A inversa de uma matrix \(2\times 2\) pode ser denotada pelo produto do recíproco do determinante da matrix pela adjunta da matrix, ou seja
\[
\begin{bmatrix}
a & b\\
c & d
\end{bmatrix}^{-1} =
\frac{1}{ad - bc}
\begin{bmatrix}
d & -b\\
-c & a
\end{bmatrix}
\]
Sendo assim, \[
(A^\top A)^{-1} = \frac{1}{n\sum x_i^2 - \left(\sum x_i\right)^2}
\begin{bmatrix}
\sum x_i^2 & -\sum x_i \\
- \sum x_i & n
\end{bmatrix}
\]
Como \(\hat{x} = (A^\top A)^{-1} A^\top b\) , temos
\[\begin{align}
\hat{x} &= \frac{1}{n\sum x_i^2 - \left(\sum x_i\right)^2}
\begin{bmatrix}
\sum x_i^2 & -\sum x_i \\
- \sum x_i & n
\end{bmatrix}
\begin{bmatrix}
\sum y_i \\
\sum x_iy_i
\end{bmatrix} \\
&=
\frac{1}{n\sum x_i^2 - \left(\sum x_i\right)^2}
\begin{bmatrix}
\sum x_i^2 \sum y_i - \sum x_i \sum x_i y_i\\
n\sum x_i y_i - \sum x_i \sum y_i
\end{bmatrix}
\end{align}\]
\[ \beta_1 = \frac{n \sum x_iy_i - \sum x_i \sum y_i}{n\sum x_i^2 - (\sum x_i)^2}\]
\[ \beta_0 = \frac{\sum y_i - \beta_1 \sum x_i}{n}\]
Método 2: \[ A^\top A \hat{x} = A^\top b\]
\[
\begin{bmatrix}
n & \sum x_i \\
\sum x_i & \sum x_i^2
\end{bmatrix}
\begin{bmatrix}
\beta_0\\
\beta_1
\end{bmatrix}=
\begin{bmatrix}
\sum y_i \\
\sum x_iy_i
\end{bmatrix}
\]
Fazendo eliminação de Gauss temos
\[
\begin{bmatrix}
n & \sum x_i \\
0 & -\frac{1}{n}(\sum x_i)^2 + \sum x_i^2
\end{bmatrix}
\begin{bmatrix}
\beta_0\\
\beta_1
\end{bmatrix}
=
\begin{bmatrix}
\sum y_i \\
-\frac{1}{n}\sum x_i \sum y_i + \sum x_iy_i
\end{bmatrix}
\]
\[ \beta_1 = \frac{n \sum x_iy_i - \sum x_i \sum y_i}{n\sum x_i^2 - (\sum x_i)^2}\]
\[ \beta_0 = \frac{\sum y_i - \beta_1 \sum x_i}{n}\]
As equações acima podem ser reorganizadas da seguinte forma \[\beta_1 = \frac{\sum_{i=1}^{n} ( x_i - \bar{x})(y_i - \bar{y}) }{\sum_{i=1}^{n} ( x_i - \bar{x})^2} \]
\[\beta_0 = \bar{y} - \beta_1 \bar{x} \] ## Avaliando a qualidade do ajuste{.scrollable}
Code
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import StandardScaler= np.array([5 ,7 ,8 ,13 ,3 ,17 ,2 ,10 ,4 ,11 ,12 ,9 ,6 ])= np.array([99 ,86 ,87 ,88 ,111 ,86 ,103 ,92 ,94 ,78 ,77 ,85 ,86 ])= x.shape[0 ]* np.sum (x* y) - np.sum (x)* np.sum (y)= x.shape[0 ]* np.sum (x** 2 ) - np.sum (x)** 2 = num/ den= (np.sum (y) - b1* np.sum (x))/ x.shape[0 ]= b0 + x* b1= "red" )for i in range (13 ):= "red" )= np.stack((x,y),axis= 1 )= StandardScaler().fit_transform(xy)print ('correlacao:' , np.corrcoef(x,y))print ('correlacao (manual):' , (x_std.T @ x_std)/ x_std.shape[0 ])
correlacao: [[ 1. -0.6973462]
[-0.6973462 1. ]]
correlacao (manual): [[ 1. -0.6973462]
[-0.6973462 1. ]]