Álgebra Linear Computacional

Aula 16: Regressão Múltipla

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento.

Predição de preços imobiliários

• Qual o valor de um imóvel?
• Existem softwares para fazer esta predição de forma automática a partir de varias características do imóvel
• Menos subjetivo, mais rápido, primeira avaliação
• Como um software desses pode ser construído?

Preço dos imóveis

• Coletamos preços de 1500 imóveis a venda no mercado de BH
• Alguns são caros, outros são baratos
• O que faz com que os preços dos imóveis variem?
• As três coisas mais importantes que afetam o valor de um imóvel…

Localização

• Localização:
  • Dividir a cidade em pequenas áreas
• Outra abordagem mais simples
  • Localização e status socio-econômico
  • Status e mensurado por renda
  • Renda e medida pelo IBGE em 2000 pequenas areas da cidade
  • Renda do do domicílio” -Então: “localização” = renda media da região onde esta o imóvel

Outras características do imóvel

• Ano da construção

• Área total do imóvel

• Número de quartos

• Numero de suítes

• Quantos aptos por andar?

• Possui salão de festas? 0 ou 1

• Possui piscina? 0 ou 1

• Ao todo, 30 características numéricas para cada um dos 1500 imoveis

Visão matricial

• Organizar os dados como vetores e matrizes
• Preços: um vetor Y de dimensão 1500
• As características: matriz 1500 x 30
  • Cada linha = um imóvel
  • 1a. coluna = renda media da região
  • 2a. coluna = ano da construção
  • 3a. coluna = área total
  • Etc.

Visão Matricial

\[Y = \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_{1459} \\ y_{1500} \end{bmatrix} \]

\[ X = \begin{bmatrix} renda_1 & área_1 & \ldots & salão_1\\ renda_2 & área_2 & \ldots & salão_2\\ \vdots & \vdots & \vdots & \vdots \\ renda_{1499} & área_{1499} & \ldots & salão_{1499}\\ renda_{1500} & área_{1500} & \ldots & salão_{1500}\\ \end{bmatrix} \] - 30 características de 1500 imóveis (matrix \(X\) de dimensão \(1500\times 30\))

Preço e uma soma ponderada

• Procuramos um modelo matemático simples que possa explicar, a partir das características, porque alguns imóveis são caros e outros são baratos
• Área total: quanto maior o imóvel, maior o preço

Influência da área

• Vamos imaginar que, APROXIMADAMENTE, o preço aumenta linearmente com a área do imóvel
• Isto é, o preço \(Y \approx a + b * área\)

Um gráfico com 150 imóveis

• Cada ponto é um imóvel
  • O eixo vertical tem os preços
  • O eixo horizontal tem as áreas
• Parece que o preço é, grosseiramente, uma função linear da área
• Isto é, \(Y\approx a + b\, área\)

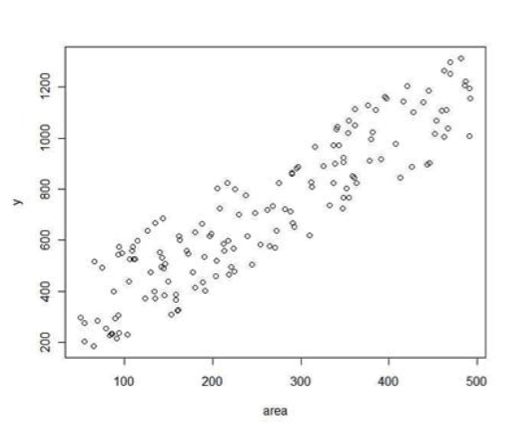
Um gráfico com 150 imóveis

• A reta no gráfico corresponde à \(Y \approx 50+2\, área\)

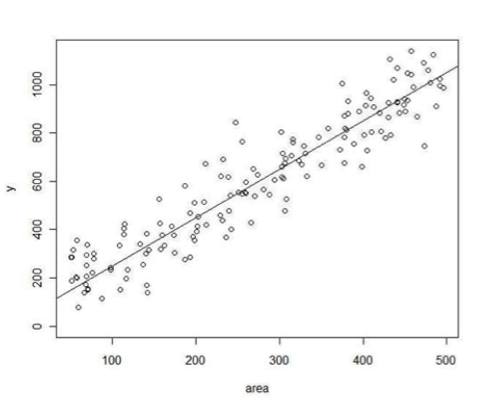
Mas a área pode não ‘explicar’ tudo

• Dois imóveis com praticamente as mesmas áreas possuem preços diferentes
• Qual a causa da diferença?
• Idade do imóvel?
• Dois imóveis com áreas iguais: se um for mais velho, provavelmente será mais barato

Ampliando o modelo inicial

• Podemos então imaginar que a idade traz um impacto adicional ao nosso modelo de preço
• Neste momento, temos \(Y \approx a + b\, área\)
• Já vimos ate mesmo que \(a\approx 50\) e \(b\approx 2\) 
• Podemos agora acrescentar o impacto de idade imaginando que:
  • \(Y = a + b\, área + c\, idade\)
• Como maior idade reduz o preço, devemos ter \(c < 0\)

Um modelo ainda mais complexo

• O preço não depende apenas da área e da idade
• Dois imóveis com a mesma área e a mesma idade podem ter preços difernetes dependedo de:
  • Localização (renda da região)
  • Número de quartos/suítes
  • Número de vagas na garagem
  • etc..
• Cada fator pode ser acrescido ao modelo inicial de forma linear

Um modelo ainda mais complexo

• Vamos considerar um modelo que, a partir das 30 características do imóvel, fornece uma predição do preço da seguinte forma
  • \(Y \approx a + b\, área + c\, idade + d \, localização + \ldots\)
• O problema é:
  • como encontrar os valores de \(a,b,c, etc.\) que torne a aproximação a melhor possível?

Formulação matemática do problema

• Queremos que cada um desses \(1500\) valores seja aproximadamente igual a uma combinação linear das \(30\) características (mais a constante \(a\))

\[\begin{align} y_1 &\approx a + b\, área_1 + c \, idade_1 + \ldots \\ y_2 &\approx a + b\, área_2 + c \, idade_2 + \ldots \\ \vdots \\ y_{1500} &\approx a + b\, área_{1500} + c \, idade_{1500} + \ldots \\ \end{align}\]

• Podemos escrever isso de forma matricial

Formulação matemática

• Para facilitar a notação no futuro, vamos escrever os pesos que multiplicam cada característica como \(b_0\) (para a constante), \(b_1\) (para a área), \(b_2\) (para idade), \(\ldots\), \(b_{30}\) para a presença ou não de são de festas

\[\begin{align} y_1 &\approx b_0 + b_1\, área_1 + b_2 \, idade_1 + \ldots + b_{30} \, salão_1\\ y_2 &\approx b_0 + b_!\, área_2 + b_2 \, idade_2 + \ldots + b_{2} \, salão_2\\ \vdots \\ y_{1500} &\approx b_0 + b_1\, área_{1500} + b_2 \, idade_{1500} + \ldots + b_{30} \, salão_{1500}\\ \end{align}\]

Formulação matemática

• Podemos empilhar tudo da seguinte maneira

\[ Y = \begin{bmatrix} y_1\\ y_2\\ \vdots \\ y_{1499}\\ y_{1500} \end{bmatrix} \approx b_0 \begin{bmatrix} 1\\1\\\vdots\\1\\1 \end{bmatrix} + b_1 \begin{bmatrix} área_1\\ área_2\\ \vdots \\ área_{1499}\\ área_{1500} \end{bmatrix} + \ldots + b_{30} \begin{bmatrix} salão_1 \\ salão_2 \\ \vdots \\ salão_{1499} \\ salão_{1500} \end{bmatrix} \]

• \(Y\) é um vetor de dimensão 1500 escrito aproximadamente como a combinação linear de 31 vetores de dimensão 1500
• Problema: encontrar os 31 coeficientes \(b_0, b_1, b_2, \ldots, b_{30}\) que tornem a aproximação acima a melhor possível

A solução do problema

• Podemos inverter uma matriz quadrada
• ou, alternativamente, resolver um sistema de equações lineares

Note

já vimos isso antes?

A solução do problema

Nosso problema é encontrar os 31 coeficientes \(b_0, b_1, b_2, \ldots, b_{30}\) que tornem a aproximação acima a melhor possível

\[ Y = \begin{bmatrix} y_1\\ y_2\\ \vdots \\ y_{1499}\\ y_{1500} \end{bmatrix} \approx b_0 \begin{bmatrix} 1\\1\\\vdots\\1\\1 \end{bmatrix} + b_1 \begin{bmatrix} área_1\\ área_2\\ \vdots \\ área_{1499}\\ área_{1500} \end{bmatrix} + \ldots + b_{30} \begin{bmatrix} salão_1 \\ salão_2 \\ \vdots \\ salão_{1499} \\ salão_{1500} \end{bmatrix} \]

Ou seja, encontrar \(b_0, b_1, b_2, \ldots, b_{30}\) tais que

\[ Y = \begin{bmatrix} y_1\\ y_2\\ \vdots \\ y_{1499}\\ y_{1500} \end{bmatrix} \approx \begin{bmatrix} 1 & área_1 & \ldots & salão_1\\ 1 & área_2 & \ldots & salão_2\\ \vdots & \vdots & \ddots& \vdots\\ 1 & área_{1499} & \ldots & salão_{1499}\\ 1 & área_{1500} & \ldots & salão_{1500}\\ \end{bmatrix} \begin{bmatrix} b_0\\ b_1 \\ \vdots \\ b_{29}\\ b_{30} \end{bmatrix} = Xb \]

onde \(b = (b_0,\ldots, b_{30})^\top\)

• Queremos \(Xb \approx Y\) como resolver isso?

Solução: um sistema linear

• Queremos encontrar \(b\) para resolver o sistema linear \(Y = Xb\)
• X é uma matriz \(1500 \times 31\) e \(Y\) é um vetor de 1500 posições
• Como \(X\) não é uma matriz quadrada, não é um sistema linear usual:
  • não tem solução, em geral

Buscaremos uma solução aproximada

• Vamos chamar a matriz \(X\) de \(A\)
• O vetor \(Y\) de \(b\)
• E o vetor \(b\) de \(x\)

Temos o problema \[Ax \approx b\]

Equações normais (Relembrando)

\[A \underbrace{x}_{\text{coeficientes}} = b + \underbrace{e}_{\text{resíduos}}\]

Ou seja, o erro é dado por \[e = Ax+b\]

Consideremos \(\hat{x}\) como a melhor solução possível, ou seja \[e = A\hat{x} - b\] é o menor erro possível

Perceba que \(A\hat{x}=p\), onde \(p\) é um vetor formado pela combinação linear das colunas de \(A\), ou seja, \(p\in C(A)\)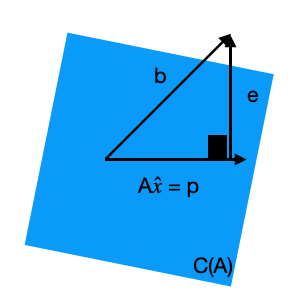

\(Ax=p\) será perpendicular ao vetor \(e\). Sendo assim, \(p^\top e = 0\). Como \(e = A\hat{x}-b\) temos

\[\begin{align} (A\hat{x})^\top (A\hat{x}-b) &= 0 \\ x^\top \underbrace{A^\top (A\hat{x} - b)}_{0} &= 0 \end{align}\]

Equação normal

\[ A^\top A \hat{x} - A^\top = 0\] ou

\[ A^\top A \hat{x} = A^\top b\]

Equações normais para Regressão Múltipla

\[ \begin{bmatrix} n & \sum x_{i1} & \sum x_{i2} & \ldots & \sum x_{i,p-1}\\ \sum x_{i1} & \sum x_{i1}x_{i1} & \sum x_{i2}x_{i1} & \ldots & \sum x_{i,p-1}x_{i1}\\ \sum x_{i2} & \sum x_{i1}x_{i2} & \sum x_{i2}x_{i2} & \ldots & \sum x_{i,p-1}x_{i2}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sum x_{i,p-1} & \sum x_{i1}x_{i,p-1} & \sum x_{i2}x_{i,p-1} &\ldots & \sum x_{i,p-1}x_{i,p-1} \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ \vdots \\ b_{p-1} \end{bmatrix} \begin{bmatrix} \sum y_{i}\\ \sum x_{i1}y_i \\ \sum x_{i2}y_{i}\\ \vdots \\ \sum x_{i,p-1}y_i \end{bmatrix} = \begin{bmatrix} \end{bmatrix} \]

Onde o vetor solução \(b\) fornece os estimadores de mínimos quadrados dos parâmetros \(\beta_i\) da equação de regressão \(y(x_1, x_2, \ldots, x_{p-1}) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_{p-1}x_{p-1} + e\)