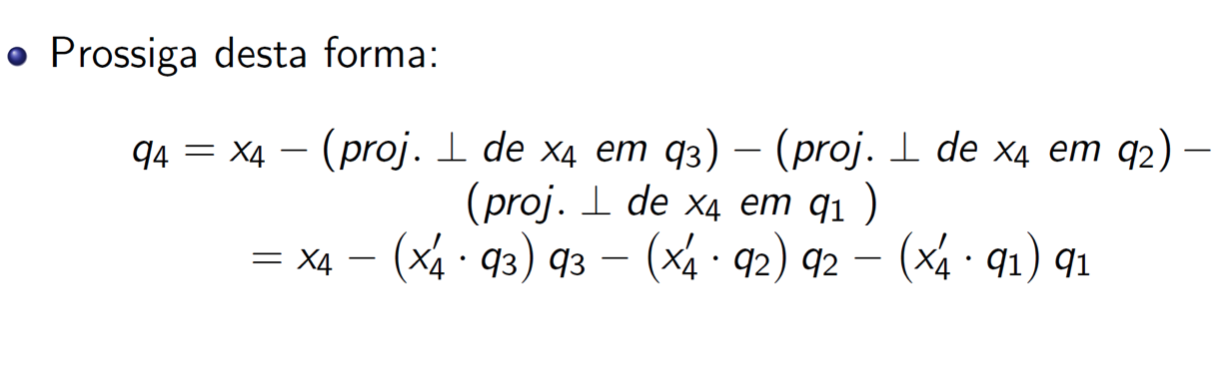Álgebra Linear Computacional

Aula 17: Coeficiente de Determinação / Resolução do problema de Mínimos Quadrados

Heitor S. Ramos
ramosh@dcc.ufmg.br

Créditos

Important

Os slides desse curso são fortemente baseados no curso do Fabrício Murai e do Erickson Nascimento

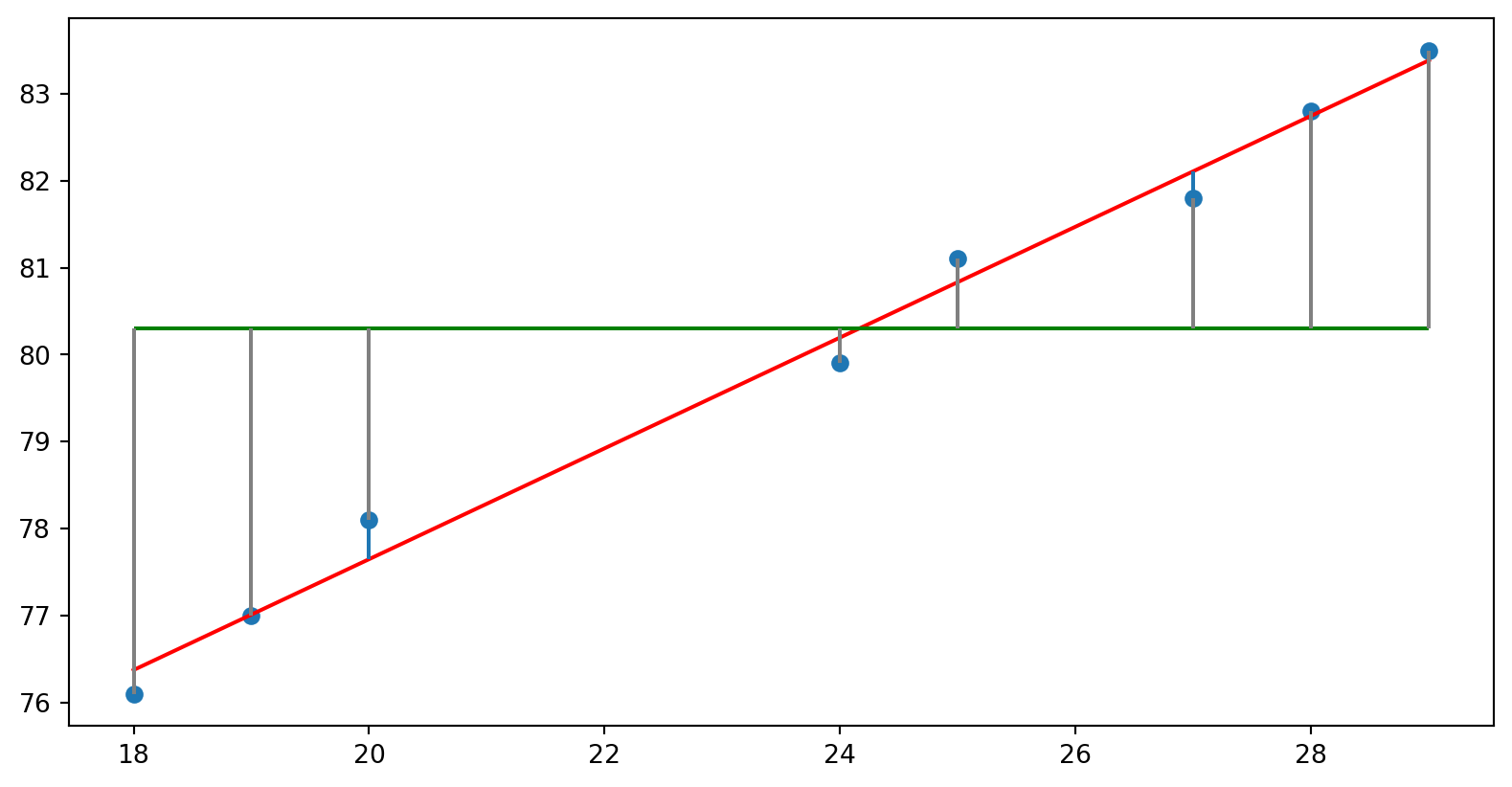
Considerações sobre o coeficiente de determinação

Como avaliar se o modelo é bom?
Em geral, quando o vetor de resíduos for “pequeno”, temos um bom ajuste \[ \Vert r \Vert^2 = \Vert Y - Y^2\Vert = \sum_{i=1}^n \left(y_i - \hat{y}\right )^2 \]

Considerações sobre o coeficiente de determinação

Mas o ajuste é bom em relação a que?
Vamos usar o modelo mais simples, a média.

Code

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
x = np.array([18,19,20,24,25,27,28,29]).reshape(-1, 1)
y = np.array([76.1, 77, 78.1, 79.9, 81.1, 81.8, 82.8, 83.5]).reshape(-1, 1)
model = LinearRegression()
model.fit(x, y)
plt.scatter(x, y)
plt.plot(x,model.predict(x), color="red")
for i in range(8):
    plt.vlines(x[i], y[i], model.predict(x)[i])
plt.hlines(80.3, np.min(x), np.max(x), color="green")
for i in range(8):
    plt.vlines(x[i], y[i], 80.3, color='grey')

Considerações sobre o coeficiente de determinação

\(\text{SQRes} = \sum_{i=1}^n (y_i - \hat{y}_i)^2\) (soma dos quadrados residual)
\(\text{SQTot} = \sum_{i=1}^n (y_i - \bar y)^2\) (soma dos quadrados total)
\(\text{SQReg} = \sum_{i=1}^n (\hat y_i - \bar y)^2\) (soma dos quadrados devido à regressão)

Dessa maneira, \[ r^2 = \frac{\text{SQTot} - \text{SQRes}}{\text{SQTot}} = 1 - \frac{\text{SQRes}}{\text{SQTot}} \] sendo \(r^2\) denominado coeficiente de determinação e satisfazendo \(0\le r^2 \le 1\)

Mínimos quadrados

\[ x^* = \text{arg}\min_x \Vert Ax -b \Vert^2 \]

Tendo como equações normais

\[A^\top A x = A^\top b\]

\[\begin{align} (A^\top A)^{-1}A^\top A x &= (A^\top A)^{-1}A^\top b \\ x &= (A^\top A)^{-1}A^\top b \end{align}\]

Moore-Penrose pseudoinversa

Considere \[A^\top A x = A^\top b\]

Toda matriz \(A = U\Sigma V^\top\)

Assim

\[ (U\Sigma V^\top)^\top (U\Sigma V^\top) x = (U\Sigma V^\top)^\top b\]

\[V\Sigma^\top U^\top U\Sigma V^\top x = V\Sigma^\top U^\top b\]

\[V\Sigma^\top \Sigma V^\top x = V\Sigma^\top U^\top b\]

\[V\Sigma^2 V^\top x = V\Sigma^\top U^\top b\]

\[V^\top V\Sigma^2 V^\top x = V^\top V\Sigma^\top U^\top b\]

\[\Sigma^2 V^\top x =\Sigma^\top U^\top b\]

\[V^\top x =\frac{\Sigma}{\Sigma^2} U^\top b\] \[x = V\Sigma^{-1} U^\top b\]

Exercício

Calcule a pseudoinversa da matrix \(A = \begin{bmatrix}1 & 2 \\ 1 & 2\end{bmatrix}\)

\[ A^\top A = \begin{bmatrix}1 & 1 \\ 2 & 2\end{bmatrix}\begin{bmatrix}1&2\\ 1&2\end{bmatrix} = \begin{bmatrix}2&4\\ 4&8\end{bmatrix}\]

Polinômio característico: \[(2- \lambda)(8 - \lambda) -16 = 0\] \[16 - 2\lambda - 8\lambda +\lambda^2 -16 = 0\]

\[ \lambda^2 - 10\lambda = 0\]

\[\lambda = 10 \text{ e } \lambda = 0\]

Calculando autovetor 1:

\[AX_1 = \lambda_1 X_1\]

\[\begin{bmatrix}2&4\\ 4 & 8\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix} = \begin{bmatrix}10x_1\\10x_2\end{bmatrix}\]

\[\begin{bmatrix}2x_1+4x_2\\ 4x_1 + 8x_2\end{bmatrix} = \begin{bmatrix}10x_1\\10x_2\end{bmatrix}\]

\[\begin{bmatrix}-8x_1+4x_2\\ 4x_1 - 2x_2\end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix}\]

\[-8x_1 = -4x_2 \Rightarrow x_1=\frac{1}{2}x_2\]

Normalizando o vetor \(X_1 = \begin{bmatrix}-\frac{1}{2}& -1\end{bmatrix}^\top\), temos \(X_1 = \begin{bmatrix}-0.4472136&-0.89442719 \end{bmatrix}^\top\)

Calculando autovetor 2 \[AX_2 = \lambda_1 X_2\]

\[\begin{bmatrix}2&4\\ 4 & 8\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix}\]

\[\begin{bmatrix}2x_1+4x_2\\ 4x_1 + 8x_2\end{bmatrix} = \begin{bmatrix}0\\0\end{bmatrix}\]

\[2x_1 = -4x_2 \Rightarrow x_1=-2x_2\]

Normalizando o vetor \(X_2 = \begin{bmatrix}-2&1\end{bmatrix}^\top\), temos \(X_2 = \begin{bmatrix}-0.89442719& 0.4472136 \end{bmatrix}^\top\)

Sendo assim, temos a decomposição SVD de \(A\) como

\[A = U\Sigma V^\top\]

com \[V^\top = \begin{bmatrix}-0.89442719& -0.4472136\\ 0.4472136& - 0.89442719\end{bmatrix}\]

\[\Sigma = \begin{bmatrix}0 & 0 \\ 0 & \sqrt{10} \end{bmatrix}\]

\[U = AV\Sigma^{-1} = \begin{bmatrix}1 & 2 \\ 1 & 2\end{bmatrix}\begin{bmatrix}-0.89442719 & -0.4472136 \\ 0.4472136& - 0.89442719 \end{bmatrix}\begin{bmatrix}0 & 0 \\ 0 & \frac{1}{\sqrt{10}} \end{bmatrix}\]

continua…. (ir para o Jupyter)

Decomposição QR

E se as colunas de \(A\) forem linearmente independentes?
Não precisamos de pseudoinversa!
Podemos procurar por matrizes fáceis de serem invertidas
- Ex: matrizes triangulares e ortogonais

Decomposição QR

Matrizes triangulares com elementos na diagonal não nulos são fáceis de inverter
Matrizes ortogonais também são fáceis de inverter \(Q^\top = Q^{-1}\)

\[Q_i^\top Q_j = \begin{cases}1, \text{ se }i=j\\ 0, \text{ se }i \neq j\end{cases}\]

A ideia é conseguir decompor a matriz \(A\) em duas matrizes fáceis de inverter, e.g., uma ortogonal e outra triangular, ou seja, \(A = QR\)

Equações normais

\(A^\top A x = A^\top b\), com \(A = QR\)

\[ (QR)^\top (QR) x = (QR)^\top b\] \[ R^\top Q^\top Q R x = R^\top Q^\top b\]

\[ R^\top R x = R^\top Q^\top b\]

\[(R^\top)^{-1}(R^\top) R x = (R^\top)^{-1}R^\top Q^\top b \]

\[ R x = Q^\top b\]

\[ (R^{-1})R x = R^{-1} Q^\top b\]

\[x = R^{-1}Q^\top b \]

Decomposição QR

Se tivermos a decomposição \(A = QR\), com \(Q^\top Q = I\) e \(R\) inversível, já sabemos como usá-la para obter os coeficientes \(\hat{\beta}_i\) em uma regressão.
Mas como obter \(A = QR\)?
Existe mais de uma maneira de obter
Vamos conhecer um algoritmo baseado na ortogonalização de Gram-Schmidt
O objetivo agora é transformar \(A\) em \(Q\), onde cada coluna \(q_i\) será ortonormal, ou seja, faremos \(q_i = \frac{A_i}{\Vert A_i\Vert}\)

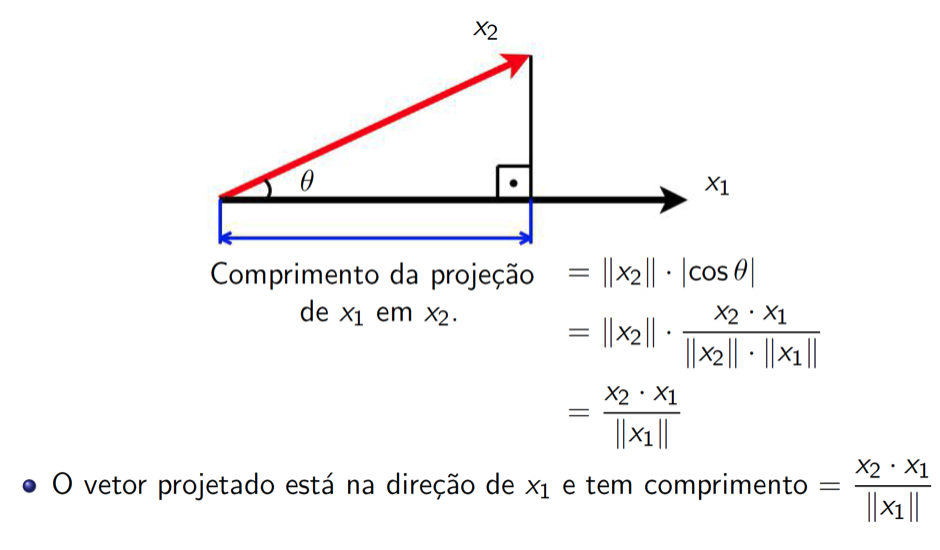
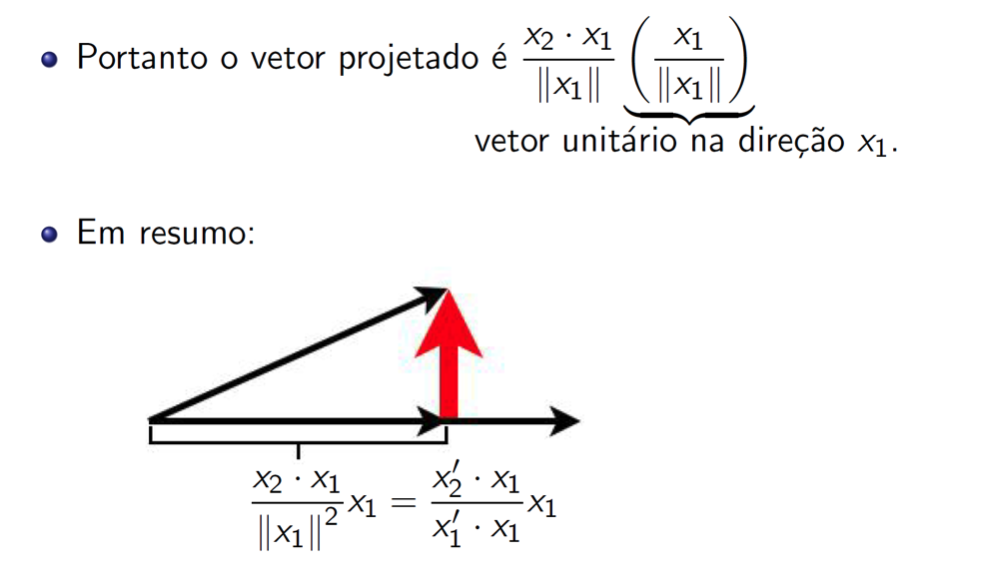
Projeção ortogonal

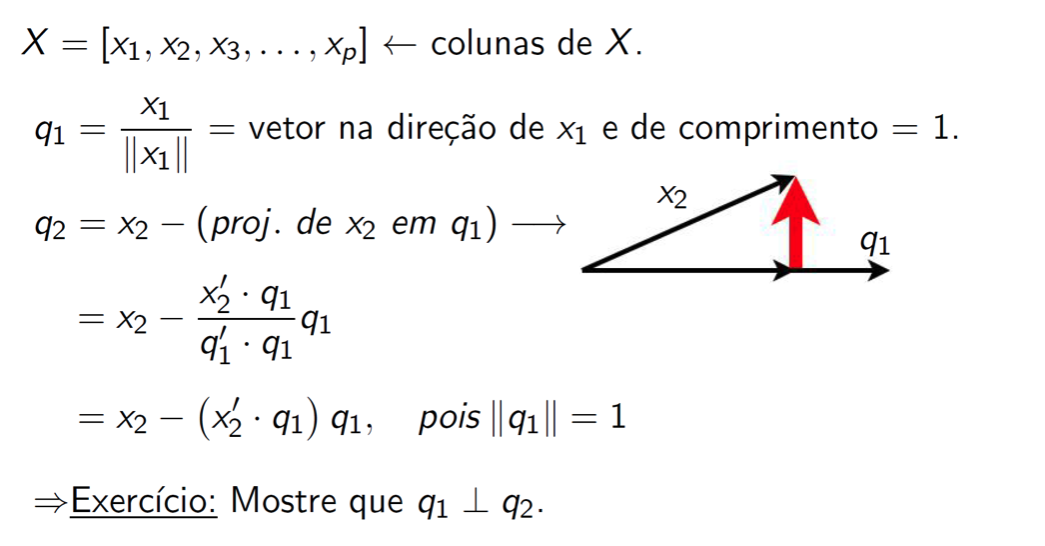
Gram-Schimidt

Como encontrar a matriz R?

\[ A = QR\]

\[Q^\top A = Q^\top Q R\]

\[R = Q^\top A\]