Álgebra Linear Computacional

Aula 18: Sistemas Lineares

Créditos

Important

Esses slides são fortemente baseados no livro do prof. Frederico Ferreira Campos, Filho

Sistemas de equações lineares

Conjunto de \(m\) equações polimoniais com \(n\) variáveis \(x_i\) de grau 1

\[\begin{align} a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n &= b_1\\ a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n &= b_2\\ a_{31}x_1 + a_{32}x_2 + \ldots + a_{3n}x_n &= b_3\\ \vdots &= \vdots \\ a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n &= b_m\\ \end{align}\]

Forma matricial

\[ \begin{bmatrix} a_{11} &a_{12} & a_{13} & \ldots & a_{1n}\\ a_{21} &a_{22} & a_{23} & \ldots & a_{2n}\\ a_{31} &a_{32} & a_{33} & \ldots & a_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} &a_{m2} & a_{m3} & \ldots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1\\ b_2 \\ b_3 \\ \vdots \\ b_n \end{bmatrix} \]

Sistemas de equações lineares

\(Ax = b\), onde \(A\) é a matriz dos coeficientes, \(x\) é o vetor solução e \(b\) é o vetor de termos independentes
Se \(A\) for uma matriz quadrada (\(n\times n\)) não singular \[A x = b \]

\[ A^{-1}Ax = A^{-1}b \]

\[ x = A^{-1}b\]

Classificação de sistemas lineares: forma da matriz

Sobredeterminado: mais equações que icógnitas

\[ A(m\times n), m\ge n\]

\[ posto(A)=n\]

Problema de quadrados mínimos lineares

\[ \underset{x}{\text{minimize}} \Vert b - Ax\Vert_2\]

possui uma única solução, chamada de solução de mínimos quadrados

Classificação de sistemas lineares: forma da matriz

Subdeterminado: existem mais icógnitas do que equações \[ A(m\times n), m <n \] \[ posto (A) = m\]
Sistema não tem solução ou existe um número infinito de soluções que satisfazem \(b- Ax = 0\)
Encontrar a solução única \(x\) que minimiza \(\Vert x \Vert_2\)
Determinar a solução de norma mínima do sistema linear
Resolver um sistema de ordem \(n\)

Classificação de sistemas lineares: número de soluções

Número de soluções depende do valor do determinante da matriz dos coeficientes
Há três situações possíveis:
- única solução
- infinitas soluções
- sem solução

Sistema com única solução

Por exemplo,

\[\begin{align} x_1 + x_2 &= 3\\ x_1 - x_2 &= -1 \end{align}\]

\[ \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 3 \\ -1 \end{bmatrix} \]

\[ A = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \]

\[ \text{det}(A) \ne 0 \] e \[ x = \begin{bmatrix} 1 &2 \end{bmatrix}^\top \]

\(\text{det}(A) \ne 0\): sistema admite única solução

Geometria de sistema com solução única

Solução de um sistema linear de ordem \(n\) é um ponto no \(\mathbb C^n\) comum aos \(n\) hiperplanos descritos por cada uma das \(n\) equações

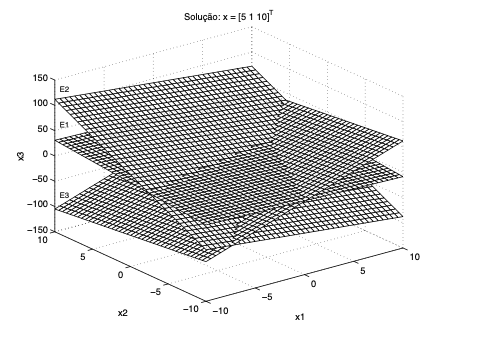
\[ \begin{bmatrix} 1 & -3 & 2 \\ -2 & 8 & -1 \\ -20 & 5 & 3 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 22 \\ -12 \\ -65 \end{bmatrix} \]

Vetor solução \(x\) é a interseção dos três planos descritos por cada uma das três equações E1, E2 e E3: \(x = \begin{bmatrix}5 & 1 & 10\end{bmatrix}^\top\)

Sistema com infinitas soluções

Por exemplo,

\[\begin{align} x_1 + x_2 &= 2 \\ 2x_1 + 2x_2 &= 4 \end{align}\]

\[ \begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \end{bmatrix} \] \[ \text{det}(A) = 0 \] \[ x = \begin{bmatrix} \theta & 2-\theta \end{bmatrix}^\top \]

\(\text{det}(A) = 0\): sistema admite infinitas soluções, uma para cada valor de \(\theta\)

Geometria de sistema com infinitas soluções

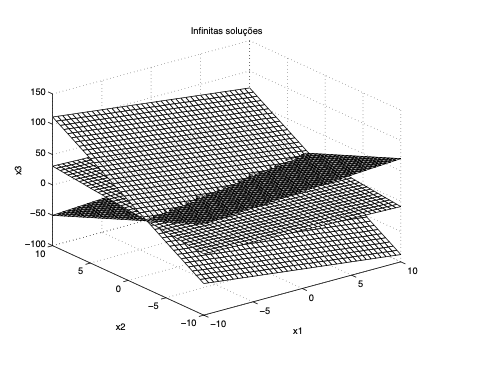
Por exemplo, \[ \begin{bmatrix} 1 & -3 & 2 \\ -2 & 8 & -1 \\ -1 & 5 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 22 \\ -12 \\ 10 \end{bmatrix} \]
Com \(\text{det}(A) = 0\), os três planos se interceptam em uma linha reta descrita por \(x = \begin{bmatrix}70-6,5\theta & 16-1,5\theta &\theta \end{bmatrix}^\top\)
Para cada valor de \(\theta\) ter-se-á uma solução do sistema linear

Sistema sem solução

Por exemplo,

\[\begin{align} x_1 + x_2 &= 1 \\ x_1 + x_2 &= -1 \end{align}\]

\[ \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix} \]

\(\text{det}(A) = 0\): sistema não tem solução

Geometria de sistema sem solução

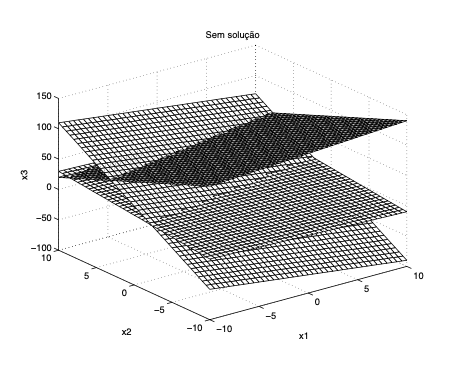
Por exemplo, \[ \begin{bmatrix} 1 & -3 & 2 \\ -2 & 8 & -1 \\ -1 & 5 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 20 \\ -10 \\ 80 \end{bmatrix} \]
Com \(\text{det}(A) = 0\) os planos não têm ponto em comum

Sistema triangular inferior

Apresenta a forma

\[ \begin{bmatrix} l_{11} & 0 & 0 & \ldots & 0 \\ l_{21} & l_{22} & 0 & \ldots & 0 \\ l_{31} & l_{32} & l_{33} & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & 0 \\ l_{n1} & l_{n2} & l_{n3} & \ldots & l_{nn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ \vdots \\ c_n \end{bmatrix} \]

Solução via substituições sucessivas

\[\begin{align} l_{11}x_1 = c_1 &\Longrightarrow x_1 = \frac{c_1}{l_{11}} \\ l_{21}x_1 + l_{22}x_2 = c_2 &\Longrightarrow x_2 = \frac{c_2 - l_{21}x_1}{l_{22}} \\ l_{31}x_1 + l_{32}x_2 + l_{33}x_3 = c_3 &\Longrightarrow x_3 = \frac{c_3 - l_{31}x_1 - l_{32}x_2}{l_{33}} \\ \vdots \end{align}\]

Sistema triangular inferior

Generalizando \[ l{n1}x_1 + l{n2}x_2 + \ldots + l_{n,n-1}x_{n-1} + l_{nn}x_n = c_n \] \[ x_n = \frac{c_n - l_{n1}x_1 - l_{n2}x_2 - \ldots - l_{n,n-1}x_{n-1}}{l_{nn}} \]
Esquematicamente \[ x_i = \frac{c_i - \sum_{j=1}^{i-1} l_{ij}x_j}{l_{ii}} \]

Exemplo de substituições sucessivas

Calcular a solução do sistema triangular inferior

\[ \begin{bmatrix} 2 & 0 & 0 & 0 \\ 3 & 5 & 0 & 0 \\ 1 & -6 & 8 & 0 \\ -1 & 4 & -3 & 9 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 4 \\ 1\\ 48 \\ 6 \end{bmatrix} \]

\[\begin{align} 2x_1 = 4 &\Longrightarrow x_1 = 2 \\ 3x_1 + 5x_2 =1 &\Longrightarrow x_2 = \frac{1-3(2)}{5} = -1 \\ x_1 - 6x_2 + 8x_3 = 48 &\Longrightarrow x_3 = \frac{48 - (2) + 6(-1)}{8} = 5\\ -x_1 + 4x_2 - 3x_3 + 9x_4 =6 &\Longrightarrow x_4 = \frac{6+(2)-4(-1)+ 3(5)}{9} = 3 \end{align}\]

Solução do sistem triangular inferior: \(x = \begin{bmatrix}2 & -1 & 5 & 3\end{bmatrix}^\top\)

Sistema triangular superior

Apresenta a forma \[ \begin{bmatrix} u_{11} & u_{12} & u_{13}& \ldots & u_{1,n-1} & u_{1n}\\ 0 & u_{22} & u_{23}& \ldots & u_{2,n-1} & u_{2n}\\ \vdots & \vdots & u_{33} & \ldots &\vdots & \vdots\\ 0 & 0 & \vdots & \ddots & u_{n-1,n-1} & u_{n-1,n}\\ 0 & 0 & 0 & \ldots & 0 & u_{nn} \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \\ x_3 \\ \vdots \\ x_{n-1} \\ x_n \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ \vdots \\ d_{n-1} \\ d_n \end{bmatrix} \]
Solução via substituições retroativas

\[\begin{align} u_{nn}x_n = d_n &\Longrightarrow x_n = \frac{d_n}{u_{nn}}\\ u_{n−1,n−1}x_{n−1} + u_{n−1,n}x_n = d_{n-1} &\Longrightarrow x_{n-1} = \frac{d_{n-1}-u_{n-1,n}x_n}{u_{n-1,n-1}}\\ \vdots \end{align}\]

Sistema triangular superior

Continuando \[\begin{align} u_{22}x_2 + u_{23}x_3 + \ldots + u_{2n}x_n = d_2 &\Longrightarrow x_2 = \frac{d_2 - u_{23}x_3 - \ldots - u_{2n}x_n}{u_{22}}\\ u_{11}x_1 + u_{12}x_2 + u_{13}x_3 + \ldots +u_{1n}x_n=d_1 &\Longrightarrow x_1 = \frac{d_1−u_{12}x_2− u_{13}x_3 − \ldots − u_{1n}x_n}{u_{11}} \end{align}\]
Esquematicamente

\[ x_i = \frac{d_i - \sum_{j=i+1}^{n} u_{ij}x_j}{u_{ii}} \] \[ i = n, n-1 , \ldots,1 \]

Exemplo de substituições retroativas

Determinar a solução do sistema triangular superior

\[ \begin{bmatrix} 5 & -2 & 6 & 1 \\ 0 & 3 & 7 & -7 \\ 0 & 0 & 4 & 5 \\ 0 & 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 1 \\ -2 \\ 28 \\ 8 \end{bmatrix} \]

\[\begin{align} 2x_4 = 8 &\Longrightarrow x_4 = 4 \\ 4x_3 + 5x_4 = 28, x_3 = \frac{28 - 5(4)}{4} &\Longrightarrow x_3 = 2 \\ 3x_2 + 7x_3 − 4x_4 = −2, x_2 = \frac{-2 -7(2) + 4(4)}{3} &\Longrightarrow x_2 = 0 \\ 5x_1− 2x_2 + 6x_3 + x_4 = 1, x_1 = \frac{1+2(0) - 6(2) - (4)}{5} &\Longrightarrow x_1 = -3 \end{align}\]

Solução do sistema triangular superior: \(x = \begin{bmatrix}-3 & 0 & 2 & 4\end{bmatrix}^\top\)

Eliminação de Gauss

O nome do método foi uma homenagem a Gauss
O processo aparece no livro chinês Nove capítulos sobre a arte matemática escrito por volta de 250 a.c.
Classes de métodos para resolução de sistemas de equações lineares: métodos diretos e iterativos
Métodos diretos: a solução exata do sistema é obtida, teoricamente, com um número finito de operações aritméticas
- Na prática, os erros de arredondamento devidos à aritmética de ponto flutuante interferem no resultado verdadeiro
Métodos iterativos: solução exata somente com um número infinito de operações
- Em cada passo dos métodos iterativos a solução é calculada com um nível de exatidão crescente
- Esse nível é limitado pelo número finito de bytes utilizados para armazenar as variáveis do programa que implementa o método iterativo

Sistemas equivalentes

Dois sistemas de equações lineares são ditos equivalentes quando possuem o mesmo vetor solução

\[ A \begin{cases} 2x_1 + 3x_2 = 8 \\ x_1 - x_2 = -1 \end{cases} \\ B \begin{cases} 2x_1 - 2x_2 = -2 \\ x_1 + 4x_2 = 9 \end{cases} \]

\[ x^A = x^B = \begin{bmatrix}1\\2\end{bmatrix} \Longrightarrow A \sim B \]

Operações l-elementares

Um sistema de equações lineares pode ser transformado em outro sistema equivalente utilizando as três operações l-elementares (operações de linha)
- trocar a ordem de duas equações
- multiplicar uma equação por uma constante
- somar uma equação à outra

Sistema triangular equivalente

Método de eliminação de Gauss

\[ \begin{bmatrix} a_{11}&a_{12}& a_{13}&\ldots&a_{1n}\\ a_{21}&a_{22}& a_{23}&\ldots&a_{2n}\\ a_{31}&a_{32}& a_{33}&\ldots&a_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ a_{n1}&a_{n2}& a_{n3}&\ldots&a_{nn}\\ \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\\vdots\\x_n \end{bmatrix} = \begin{bmatrix} b_1\\b_2\\b_3\\\vdots\\b_n \end{bmatrix} \sim \]

\[ \begin{bmatrix} u_{11}&a_{12}& u_{13}&\ldots&u_{1n}\\ 0&u_{22}& u_{23}&\ldots&u_{2n}\\ 0&0& u_{33}&\ldots&u_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0&0& 0&\ldots&u_{nn}\\ \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\\vdots\\x_n \end{bmatrix} = \begin{bmatrix} b_1\\b_2\\b_3\\\vdots\\b_n \end{bmatrix} \]

Transformação \(Ax = b \sim Ux = d\)
Solução do sistema triangular superior \(Ux=d\) obtida pelas substituições retroativas
Vetor resíduo \(r = b - Ax\)

Exemplo

Resolver o sitema abaixo pelo método da solução de Gauss e verificar a exatidão da solução

\[ \begin{bmatrix} 1 & -3 & 2\\ -2 & 8 & -1\\ 4 & -6 & 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 11\\ -15 \\ 29 \end{bmatrix} \] - Eliminar os elementos da primeira coluna \[ \begin{bmatrix} 1 & -3 & 2\\ 0 & 2 & 3\\ 0 & 6 & -3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 11\\ 7 \\ -15 \end{bmatrix} \]

Eliminar os elementos da segunda coluna \[ \begin{bmatrix} 1 & -3 & 2\\ 0 & 2 & 3\\ 0 & 0 & -12 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 11\\ 7 \\ -36 \end{bmatrix} \]
Encontrar o vetor solução através de substituições retroativas \[\begin{align} -12x_3 = -36 &\Longrightarrow x_3 = 3\\ 2x_2 + 3x_3 = 7 &\Longrightarrow x_2 = -1 \\ x_1 - 3x_2 + 2x_3 = 11 &\Longrightarrow x_1 = 2 \end{align}\]
Vetor solução do sistema: \(x = \begin{bmatrix} 2 & -1 &3\end{bmatrix}^\top\)
Vetor resíduo: \(r = b - Ax\)

\[ r = \begin{bmatrix} 11 \\ -15 \\ -29 \end{bmatrix} - \begin{bmatrix} 1 & -3 & 2 \\ -2 & 8 & -1 \\ 4 & -6 & 5 \end{bmatrix} \begin{bmatrix} 2 \\ -1 \\ 3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\0 \end{bmatrix} \]

Solução exata

Tip

Como calcular o determinante de uma matriz triangular?

Pivotação parcial

Método de Gauss falha quando pivô é nulo
Consiste em escolher como pivô o maior elemento em módulo da coluna cujos elementos serão eliminados
A pivotação parcial garante que o pivô seja não nulo, exceto quando a matriz for singular
Todos os multiplicadores satisfazem \[ -1 \le m_{ij}\le 1 \]
Multiplicadores grandes podem ampliar os erros de arredondamento

Exemplo de pivotação parcial

Resolver o sistema pelo método de Gauss com pivotação parcial \[ \begin{bmatrix} 1 & -3 & 2\\ -2 & 8 & -1\\ 4 & -6 & 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 11\\ -15 \\ 29 \end{bmatrix} \] - Escolha do pivô: (elemento \(a_{31}\))

Escolha do Multiplicador \(m_{11} = \frac{a_{11}}{a_{31}} = 0,25\)
Escolha do Multiplicador \(m_{21} = \frac{a_{21}}{a_{31}} = -0,5\)
Eliminar os elementos da primeira coluna \[ \begin{bmatrix} 0 & -1,5 & 0,75\\ 0 & 5 & 1,5\\ 4 & -6 & 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 3,75\\ -0,5 \\ 29 \end{bmatrix} \]

Para eliminar o elemento da segunda coluna, escolhe-se o maior elemento em módulo desta coluna, sem considerar o elemento da linha pivotal \(L3\). Sendo assim, o pivô será o elemento \(a_{22}\)

Escolha do multiplicador \(m_{12} = \frac{a_{12}}{a_{22}} = -0,3\)
Eliminar os elementos da segunda coluna \[ \begin{bmatrix} 0 & 0 & 1,2\\ 0 & 5 & 1,5\\ 4 & -6 & 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 3,6\\ -0,5 \\ 29 \end{bmatrix} \]

Para que a matriz fique triangular superior, podemos trocar as linhas \(L3\) e \(L1\) \[ \begin{bmatrix} 4 & -6 & 5\\ 0 & 5 & 1,5\\ 0 & 0 & 1,2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 29\\ -0,5 \\ 3,6 \end{bmatrix} \]

Por que o determinante ficou diferente? (simétrico)

Trocar po sição de duas linhas: \(\text{det}(A) = -\text{det}(A')\)
Multiplicar todos os elementos de uma linha por uma constante \(k\): \(\text{det}(A) = k\text{det}(A')\)
Somar o múltiplo escalar de uma linha à outra linha: \(\text{det}(A) = \text{det}(A')\)