Álgebra Linear Computacional

Aula 21: Análise de Convergência

Créditos

Important

Esses slides são fortemente baseados no livro do prof. Frederico Ferreira Campos, Filho.

Análise de Convergência

Seja o erro \(\epsilon^k\) na \(k\)-ésima iteração \[ \epsilon^k = x^k - x^*, \]
\(x^*\): solução exata do sistema \(Ax = b\) de ordem \(n\) e
\(x^k\): aproximação da solução
Substituindo a equação acima para \(\epsilon^{k+1}\) em \(x^{k+1} = M x^k +c\), temos \[ \epsilon^{k+1} = x^{k+1} - x^* = Mx^k + c - x^*. \]
Sendo \(x^k = \epsilon^k + x^*\), \[ \epsilon^{k+1} = M(\epsilon^k + x^*) + c - x^*, \] \[ \epsilon^{k+1} = M(\epsilon^k) + (Mx^*+c - x^*). \]
Tomando o limite temos, \[ \lim_{k\rightarrow \infty}x^{k+1} =\lim_{k\rightarrow \infty} Mx^k + c \longrightarrow x^* = Mx^* +c. \]
A propagação de erro é da forma \[ \epsilon^{k+1} = M \epsilon^k \]
Sendo \(\lambda_i\) um autovalor de M e \(v_i\) o seu autovetor correspondente, \[ Mv_i = \lambda_iv_i, i=1,2,\ldots,n \] ou \[ MV = V\Lambda \]
\(\Lambda = \text{diag}(\lambda_1, \lambda_2,\ldots,\lambda_n)\): matriz diagonal contendo os autovalores
\(V\): matriz composta pelos autovetores \(v_i\).
Expressando o vetor erro inicial \(\epsilon^0\) como uma combinação dos autovetores \(V\) de \(M\) \[ \epsilon^0 = Vc \]
onde \(c\): um vetor de coeficientes obtido pela solução do sistema linear acima
substitindo em \(\epsilon^{k+1} = M \epsilon^k\) \[ \epsilon^1 = M\epsilon^0 = MVc = V\Lambda c \] \[ \epsilon^2 = M\epsilon^1 = MV\Lambda c = V\Lambda^2 c \] ou seja,

\[ \epsilon^k = V\Lambda^k c \] \[ \begin{bmatrix} \epsilon^k_1\\\epsilon^k_2\\ \ldots \\ \epsilon^k_n \end{bmatrix} = \begin{bmatrix} v_{11} & v_{12} & \ldots & v_{1n}\\ v_{21} & v_{22} & \ldots & v_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ v_{n1} & v_{n2} & \ldots & v_{nn}\\ \end{bmatrix} \begin{bmatrix} c_1\lambda_1^k \\ c_2\lambda_2^k \\ \vdots \\ c_n\lambda_n^k \end{bmatrix} \] - Quando \(k\) aumentar, o vetor erro \(\epsilon^k\) irá reduzir se, e somente se, todos os autovalores \(\lambda_i\) da matriz de iteração \(M\) forem menores que a unidade - A taxa de convergência será controlada pela magnitude do maior autovalor em módulo, o chamado raio espectral \(\rho(M)\)

Exemplo 1

Seja o sistema \(Ax = b\) e sua solução exata \(x^*\)

\[ \begin{bmatrix} 10 & 3 & -2 \\ 2 & 8 & -1 \\ 1 & 1 & 5 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 57\\20\\-4 \end{bmatrix} \] e \[ x^* = \begin{bmatrix} 5 \\ 1 \\ -2 \end{bmatrix} \]

Usando Gauss-Seidel obtemos a seguinte equação de recorrência \(x^{k+1} = Sx^k + d\)

\[ S= \begin{bmatrix} 0 & -0,300 & 0,200 \\ 0 & 0,075 & 0,075 \\ 0 & 0,045 & -0,055 \end{bmatrix} \] e \[ d = \begin{bmatrix} 5,700 \\ 1,075 \\ -2,155 \end{bmatrix} \text{ e } x^0 = \begin{bmatrix} 5,7 \\ 2,5 \\ -0,8 \end{bmatrix} \]

Assim, temos que o vetor erro inicial é \(\epsilon^0 = x^0 - x^* = \begin{bmatrix}0,7 & 1,5 & 1,2\end{bmatrix}^\top\)
Calculando os autovalores \(\Lambda\) da matriz de iteração \(S\) e seus respectivos autovalores \(V\) temos

\[\Lambda = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0,09718 & 0 \\ 0 & 0 & -0,07718 \end{bmatrix} \]

\[ V = \begin{bmatrix} 1 & -0,92174 & -0,97074 \\ 0 & 0,37189 & -0,10615 \\ 0 & 0,10997 & 0,21538 \end{bmatrix} \]

Sendo assim, o erro na \(k\)-ésima iteração é \[ \begin{bmatrix} \epsilon^k_1 \\\epsilon^k_2\\ \epsilon^k_3 \end{bmatrix} = \begin{bmatrix} 1 & -0,92174 & -0,97074 \\ 0 & 0,37189 & -0,10615 \\ 0 & 0,10997 & 0,21538 \end{bmatrix} \begin{bmatrix} 8,19997(0)^k \\ 4,90841(0,09718)^k \\ 3,06538(−0,07718) ^k \end{bmatrix} \]
Sendo o vetor \(c\) a solução do sistema linear \(Vc = \epsilon^0\)
Calcula-se o vetor erro \(\epsilon^k\) a cada iteração

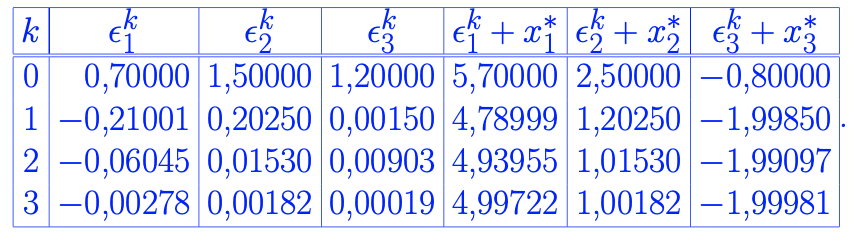
O processo converge pois \(\vert \lambda_i\vert < 1 \forall i\)

\[ \lim_{k\rightarrow \infty} \lambda_i^k = 0 \Rightarrow \lim_{k\rightarrow \infty} \epsilon^k = 0 \]

Solução divergiria se pelo menos um \(\vert \lambda_i\vert>1\)

\[ \lim_{k\rightarrow \infty} \lambda_i^k = \infty \Rightarrow \lim_{k\rightarrow \infty} \epsilon^k = \infty \]

Comparação entre os métodos iterativos estacionários

Matriz dos coeficientes \(A\) com diagonal estritamente dominante: solução converge pelos métodos de Jacobi e Gauss-Seidel
Se \(A\) não for diagonalmente dominante: previsão de convergência feita usando o raio espectral \(\rho(M)\) da matriz de iteraçao
Neste caso, um método pode convergir e o outro não

Exemplo 2

Verificar se o sistema abaixo pode ser resolvido pelo método de Jacobi ou de Gauss-Seidel \[ \begin{bmatrix} 0,5 & 0,6 & 0,3 \\ 1 & 1 & 1 \\ 0,4 & -0,4 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 0,2 \\ 0 \\ -0,6 \end{bmatrix} \] - A matrix \(A\) não é diagonal estritamente dominante - Matrizes de iteração \[ J = -D^{-1}(E + F) = \begin{bmatrix} 0 & -1,2 & -0,6 \\ -1 & 0 & -1 \\ -0,4 & 0,4 & 0 \end{bmatrix} \]

\[ S = -(D + E)^{-1}F= \begin{bmatrix} 0 & -1,2 & -0,6 \\ 0 & 1,2 & -0,4 \\ 0 & 0,96 & 0,08 \end{bmatrix} \]

\(\rho(J) = 1,1200\) e \(\rho(S) = 0,6928\)
O sistema converge para Gauss-Seidel, mas não converge para Jacobi pois \(\rho(J)>1\) e \(\rho(S)<1\)

Exemplo 3

Verificar se o sistema abaixo pode ser resolvido pelo método de Jacobi ou de Gauss-Seidel \[ \begin{bmatrix} 0,5 & 0,6 & 0,3 \\ 1 & -1 & 1 \\ 0,4 & -0,4 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 0,2 \\ 0 \\ -0,6 \end{bmatrix} \] - A matrix \(A\) não é diagonal estritamente dominante - Matrizes de iteração \[ J = -D^{-1}(E + F) = \begin{bmatrix} 0 & -1,2 & -0,6 \\ -1 & 0 & 1 \\ -0,4 & 0,4 & 0 \end{bmatrix} \]

\[ S = -(D + E)^{-1}F= \begin{bmatrix} 0 & -1,2 & -0,6 \\ 0 & -1,2 & 0,4 \\ 0 & 0 & 0,4 \end{bmatrix} \]

\(\rho(J) = 0,8266\) e \(\rho(S) = 1,2000\)
O sistema converge para Jacobi, mas não converge para Gauss-Seidel pois \(\rho(J)<1\) e \(\rho(S)>1\)

Velocidade de Convergência

Vetor erro \(e^k = V\Lambda^k c\)
Quanto menor o valor de \(\rho(M)\), masi rápido convergirá o método iterativo
Matrizes iteração para um determinado sistema: \[ J = -D^{-1}(E + F) = \begin{bmatrix} 0 & -0,3 & 0,2 \\ -0,25 & 0 & 0,125 \\ -0,2 & -0,2 & 0 \end{bmatrix} \]

\[ S = -(D + E)^{-1}F= \begin{bmatrix} 0 & -0,3& 0,2 \\ 0 & 0,075 & 0,075 \\ 0 & 0,045 & -0,055 \end{bmatrix} \] - Raios espectrais: \((\rho(S)=0,0972 ) < (\rho(J)=0,2725)\) - Método de Gauss-Seidel converge mais rápido - Gasta 6 iterações contra 9 iterações do método de Jacobi