Code
Norma infinito de H: 2.083333333333333
Norma infinito de H^-1: 13619.999999998996Aula 22: Análise de Erros na Solução de Sistemas Lineares
Important
Esses slides são fortemente baseados no livro do prof. Frederico Ferreira Campos, Filho.
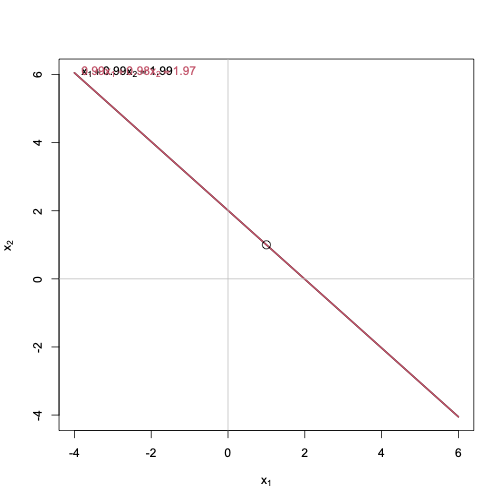
\(A = \begin{bmatrix} 1 & 0,99 \\ 0,99 & 0,98 \end{bmatrix}\) e \(b= \begin{bmatrix} 1,99 \\ 1,97 \end{bmatrix}\)
\(A = \begin{bmatrix} 1 & 0,99 \\ 0,99 & 0,98 \end{bmatrix}\) e \(b= \begin{bmatrix} 1,99 \\ 1,97 \end{bmatrix}\)

\[ \text{condição}(A) = \kappa(A) = \Vert A\Vert \Vert A^{-1}\Vert \]
\[ A = \begin{bmatrix} 1 & 0,99 \\ 0,99 & 0,98 \end{bmatrix} \] e \[ B = \begin{bmatrix} 5 & 3 & 0 \\ -1 & 8 & 6 \\ 4 & 2 & 9 \end{bmatrix} \]
\[\lambda(A) = \begin{bmatrix}19801& -5,0504\cdot 10^{-5}\end{bmatrix}\]
\[ \kappa_2(A) = \frac{\vert 1,9801\vert}{\vert -5,0504\cdot 10^{-5}\vert} = 3,9206\cdot 10^4 \] e \[ \lambda(B^\top B) = \begin{bmatrix}1,7423\cdot 10^2 & 3,7222\cdot 10^1 & 2,4548\cdot 10^1\end{bmatrix} \] \[ \kappa_2(B) = \sqrt{\frac{1,7423\cdot 10^2}{2,4548\cdot 10^1}} = 2,6641 \]
\[ H_n = \frac{1}{i+j-1}, i,j=1,2,\ldots,n \]
\(H2 = \begin{bmatrix}1&1/2 \\ 1/2 & 1/3\end{bmatrix}\) e \(H_3 = \begin{bmatrix}1 & 1/2 & 1/3 \\ 1/2 & 1/3 & 1/4 \\ 1/4 & 1/4 & 1/5\end{bmatrix}\)
Norma infinito de H: 2.083333333333333
Norma infinito de H^-1: 13619.999999998996| n | \(\Vert H_n\Vert_\infty\) | \(\Vert H_n^{-1}\Vert_\infty\) | \(\kappa_\infty(H_n)\) |
|---|---|---|---|
| 1 | \(1,00000\) | \(1,00000\cdot10^{0}\) | \(1,00000\cdot10^{0}\) |
| 2 | \(1,50000\) | \(1,80000\cdot10^{1}\) | \(2,70000\cdot10^{1}\) |
| 3 | \(1,83333\) | \(4,08000\cdot10^{2}\) | \(7,48000\cdot10^{2}\) |
| 4 | \(2,08333\) | \(1,36200\cdot10^{4}\) | \(2,83750\cdot10^{4}\) |
| 5 | \(2,28333\) | \(4,13280\cdot10^{5}\) | \(9,43656\cdot10^{5}\) |
| 6 | \(2,45000\) | \(1,18654\cdot10^{7}\) | \(2,90703\cdot10^{7}\) |
| 7 | \(2,59286\) | \(3,79965\cdot10^{8}\) | \(9,85195\cdot10^{8}\) |
| 8 | \(2,71786\) | \(1,24631\cdot10^{10}\) | \(3,38728\cdot10^{10}\) |
| 9 | \(2,82897\) | \(3,88712\cdot10^{11}\) | \(1,09965\cdot10^{11}\) |
| 10 | \(2,92897\) | \(1,20716\cdot10^{13}\) | \(3,53574\cdot10^{13}\) |
\[\delta x = A^{-1} \delta b\]
\[ \Vert A\Vert\Vert x\Vert \ge \Vert b\Vert \] e \[ \Vert \delta x \Vert \le \Vert A^{-1}\Vert \Vert \delta b\Vert \]
\[ \frac{\Vert \delta x\Vert}{\Vert x\Vert} \le \Vert A\Vert \Vert A^{-1}\Vert \frac{\Vert \delta b\Vert}{\Vert b\Vert} \] \[ \frac{\Vert \delta x\Vert}{\Vert x\Vert} \le \kappa(A)\frac{\Vert \delta b\Vert}{\Vert b\Vert} \]
\(A = \begin{bmatrix}1&0,99\\ 0,99 & 0,98\end{bmatrix}\), \(b = \begin{bmatrix}1,99 \\ 1,97\end{bmatrix}\) e \(\delta b= \begin{bmatrix}0\\ 0,01\end{bmatrix}\)
\[ Ax + A\delta x + \delta Ax + \delta A \delta x = b \]
\[ A\delta x = -\delta A(x+\delta x) \]
\[ \Vert \delta x\Vert \le \Vert A^{-1}\Vert \Vert \delta A\Vert \Vert x + \delta x\Vert \] ou
\[ \frac{\delta x}{x + \delta x}\le \kappa(A)\frac{\Vert \delta A\Vert}{\Vert A\Vert} \]
\(A = \begin{bmatrix}1&0,99\\ 0,99 & 0,98\end{bmatrix}\), \(b = \begin{bmatrix}1,99 \\ 1,97\end{bmatrix}\) e \(\delta A= \begin{bmatrix}0 & 0\\0& 0,01\end{bmatrix}\)
\[ \frac{\Vert\delta x\Vert_2}{\Vert x + \delta x\Vert} \le \kappa_2(A)\frac{\Vert\delta A\Vert_2}{\Vert A\Vert_2} = 1,9206\cdot 10^4\frac{10^{-2}}{1,9801} \]
\[ \frac{\Vert\delta x\Vert_2}{\Vert x + \delta x\Vert} \le 1,9800\cdot 10^2 \]
Com a perturbação \(\delta A\), x variou de \(x=\begin{bmatrix}1&1\end{bmatrix}^\top\) para \(\tilde{x} = \begin{bmatrix}2&-1/99\end{bmatrix}^\top\)
Variação na solução \(\delta x = \begin{bmatrix}2-1 & -1/99 -1\end{bmatrix}^\top\)
Erro relativo real
\[ \frac{\Vert\delta x\Vert_2}{\Vert x + \delta x\Vert} = \frac{1,4214}{2,0000} = 7,1070\cdot 10^{-1} \]
Os sistemas lineares podem ser:
